G(x)=(x-3)•(16-4x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow \)\(\left[\begin{array}{} x-3=0 \\ 16-4x=0 \end{array} \right.\)
\(\Leftrightarrow \)\(\left[\begin{array}{} x=3\\ x=4 \end{array} \right.\)
Vậy S = {3,4}

h(x)=f(x)-g(x)= 5x^3+3x^2-9x+1-4x3+7x3+6x+16
=8x3+3x2-3x+17
Ta có: \(f\left(x\right)=5x^3+3x^2-9x+1\)
\(g\left(x\right)=4x^3-7x^3-6x-16\)
\(h\left(x\right)=f\left(x\right)-g\left(x\right)=\left(5x^3+3x^2-9x+1\right)-\left(4x^3-7x^3-6x-16\right)\)
\(=5x^3+3x^2-9x+1-4x^3+7x^3+6x+16\)
\(=8x^3+3x^2-3x+17\)

Ta có :
\(f\left(x\right)-g\left(x\right)=4x+\frac{16}{3}\)
\(\Rightarrow4x+\frac{16}{3}=0\)
\(\Rightarrow4x=0-\frac{16}{3}\)
\(\Rightarrow4x=\frac{-16}{3}\)
\(\Rightarrow x=\frac{-16}{3}\div4\)
\(\Rightarrow x=\frac{-4}{3}\)
Vậy nghiệm của đa thức f (x) - g(x) là \(\frac{-4}{3}\)

=>x-3=0 hoặc 16-4x=0
=>x=3 hoặc x=4
Vậy tập nghiệm của phương trình là{3,4}
Để g(x)=0 thì x-3=0 hoặc 16-4x=0
Xét x-3=0 thì x=3
Xét 16-4x=0 thì x=4
Vậy đa thức có 2 nghiệm là x1=3 và x2=4

a) Đặt G(x) = (x-3)(16-x)
Trường hợp 1: x - 3 = 0
x = 3
Trường hợp 2: 16 - 4x = 0
4x = 16
x = 4
Vậy x = 2 hoặc x = 4
Câu b tương tự

`f( x) = 3x -6`
`-> 3x-6=0`
`=> 3x=0+6`
`=> 3x=6`
`=>x=6:3`
`=>x=2`
__
`h( x) =-5 x+30`
`-> -5x +30=0`
`=> -5x=0-30`
`=>-5x=-30`
`=>x=6`
__
`g(x) = ( x-3)(16-4x)`
`-> ( x-3)(16-4x)=0`
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\16-4x=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\4x=16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
__
`k( x) = x^2-81`
`->x^2-81=0`
`=> x^2=81`
`=> x^2 =+-9^2`
\(\Rightarrow\left[{}\begin{matrix}x=9\\x=-9\end{matrix}\right.\)
\(3x-6=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Vậy nghiệm của đa thức f(x) là \(x=2\)
\(-5x+30=0\)
\(\Rightarrow-5x=-30\)
\(\Rightarrow x=6\)
Vậy nghiệm của đa thức h(x) là \(x=6\)
\(\left(x-3\right)\left(16-4x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\16-4x=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\4x=16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
Vậy nghiệm của đa thức g(x) là \(x\in\left\{3;4\right\}\)
\(x^2-81=0\)
\(\Rightarrow x^2=81\)
\(\Rightarrow\left[{}\begin{matrix}x=9\\x=-9\end{matrix}\right.\)
Vậy nghiệm của đa thức k(x) là \(x\in\left\{9;-9\right\}\)

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
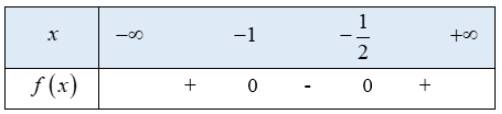
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
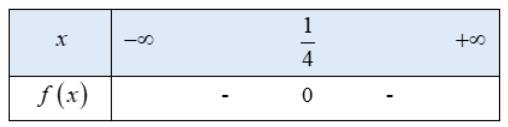
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

g)G(x)=x^3-4x=0
=>x(x^2-4)=0
=>\(\left[{}\begin{matrix}x=0\\x^2-4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x^2=4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=\sqrt{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy nghiệm của đa thức G(x) là 0 hoặc 2
h) H(x)=5x^3-4x^2-3x^3+3x^2-2x^3+x=0
=>(5x^3-3x^3-2x^3)+(-4x^2+3x^2)+x
=>x-x^2=0
=>x(1-x)
=>\(\left[{}\begin{matrix}x=0\\1-x=0\end{matrix}\right.\) =>\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy nghiệm của đa thức H(x) là 0 hoặc 1