cho tam giác ABC có AB>AC.Kẻ tia phân giác BN của góc ABC (N thuộc AC) CM là tia phân giác của ACB (M thuộc AB) BM và CM cắt nhau tại I . So sánh IB và IC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CT
cẩm tú lê
26 tháng 2 2022
Đúng(1)
Những câu hỏi liên quan
30 tháng 6 2022
Bài 1:
Xét ΔABC có BD là phân giác
nen AD/AB=CD/BC
mà AB<BC
nên AD<CD
30 tháng 6 2022
a: Ta có: AB>AC
nên \(\widehat{ACB}>\widehat{ABC}\)
=>\(\widehat{ICB}>\widehat{IBC}\)
hay IB>IC
b: TH1: ΔABC cân tại C
mà CM là phân giác
nên MA=MB
TH2: ΔABC không cân tại C
=>MA<>MB
D
24 tháng 3 2016
a) từ I kẻ IK sao cho KIB=NIB(K thuộc BC)
xét tam giác INB và tam giác IKB có:
NBI=CBI(gt)
IB(chung)
NIB=IKB
suy ra tam giác INB=IKB(g.c.g)
suy ra NIB=BIC
CM tương tự ta có tam giác MIC=KIC(c.g.c)suy ra MIC=KIC
mà NIB=MIC suy ra NIB=BIK=KIC=180/3=60 độ
suy ra BIN=60 độ
7 tháng 3 2023
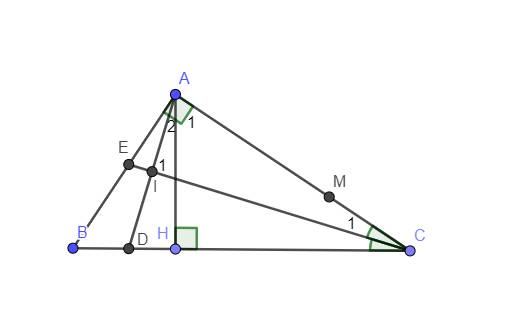
`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
21 tháng 1
a:
ΔABC vuông tại A nên BC là cạnh lớn nhất
=>AC<BC
mà AB<AC
nên AB<AC<BC
Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Ta có: \(\widehat{ABI}=\widehat{CBI}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACI}=\widehat{BCI}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ACB}< \widehat{ACB}\)
nên \(\widehat{ICB}< \widehat{IBC}\)
Xét ΔIBC có \(\widehat{ICB}< \widehat{IBC}\)
mà IB,IC lần lượt là cạnh đối diện của các góc ICB và góc IBC
nên IB<IC
TN
21 tháng 8 2015
ta co goc A+ B+ C=180 ( tong 3 goc trong tam giac ABC)
--> B+C=180-60=120
ta co : goc B1+goc BIC+goc C1=180 ( tong 3 goc trong tam giac BIC)
ma goc B1=1/2 B va C1=1/2 C ( BI va CI la tia p/g goc B va C)
nen 1/2 B+1/2C+ goc BIC=180
1/2 ( B+C) +goc BIC =180
1/2.120+goc BIC=180
60+ goc BIC=180
-> goc BIC=180- 60 =120
--> I1=I2= I : 2= 120:2 =60 ( IF la tia p.g goc BIC)
ta co : goc BIC + goc I 3=180 ( 2 goc ke bu)
--> 120 +I3 =180
--> I3 =180-120=60
ta co : goc I4= goc I3 ( 2 goc doi dinh)
goc I1=goc I3 (=60)
--> goc I4= goc I1--> IB la tia p/g goc EIF
ta co I2=I3 ( = 60)--> IC la tia p/g goc DIF
30 tháng 6 2022
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AHchung
Do đo: ΔAHB=ΔAHC
b: HB=HC=BC/2=3cm
=>AH=4cm
c: Xét ΔABM và ΔACN có
góc ABM=góc ACN
AB=AC
góc BAM chung
Do đó: ΔABM=ΔACN
Suy ra BM=CN
Xét ΔNBC và ΔMCB có
NB=MC
NC=MB
BC chung
Do đo: ΔNBC=ΔMCB
Suy ra: góc KBC=góc KCB
=>ΔKBC cân tại K
=>KB=KC
=>KN=KM
hay ΔKNM cân tại K
d: Xét ΔABC có AN/AB=AM/AC
nên NM//BC
4 tháng 11 2015
Các bạn giải hộ mình bài này nhé http://olm.vn/hỏi-đáp/question/264598.html