Cho đường tròn $(O)$, các bán kính $OA$ và $OB$. Trên cung nhỏ $AB$ lấy các điểm $M$ và $N$ sao cho $AM = BN$. Gọi $C$ là giao điểm của các đường thẳng $AM$ và $BN$. Chứng minh rằng:
a) $OC$ là tia phân giác của \(\widehat{AOB}\).
b) \(OC\perp AB\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 5 2019
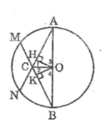
Kẻ OH ⊥ AM, OK ⊥ AN
Ta có: AM = AN (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCH và OCK, ta có:
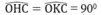
OC chung
OH = OK (chứng minh trên)
Suy ra: ∆ OIH = ∆ OIK (cạnh huyền, cạnh góc vuông)
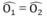
Xét hai tam giác OAH và OBH, ta có:
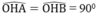
OA = OB
OH = OK (chứng minh trên)
Suy ra: ∆ OAH = ∆ OBH (cạnh huyền, cạnh góc vuông)
CM
25 tháng 2 2019
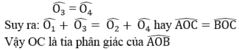
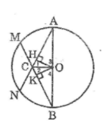
Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)
Suy ra: OC ⊥ AB
14 tháng 2 2020
Xét đường tròn tâm (O) có AM=BN
Từ đó ta suy ra OE=OD (tính chất quan hệ giữa đường kính và dây cung)
Xét tam giác vuông AOD và tam giác vuông BOE có:
OA=OB(cùng bằng bán kính)
OE=OD(chứng minh trên)
=> ΔAOD = ΔBOE (cạnh huyền-cạnh góc vuông)
=> ∠O1 = ∠O4 (2 góc tương ứng)(1)
Tương tự ta có: ∠O2 = ∠O3 (2)
Ta có: ∠AOC = ∠O1 + ∠O2
∠BOC = ∠O3 + ∠O4
Từ (1) và (2) ta suy ra ∠AOC= ∠BOC
Suy ra OC là tia phân giác của góc AOB.
Xét tam giác OBF và tam giác OAF có:
∠AOC = ∠BOC (chứng minh trên)
OA=OB
OF: chung
Suy ra ΔOBF = ΔOAF (c-g-c)
=> BF=AF( 2 cạnh tương ứng)
=> OC ⊥ AB
HH
16 tháng 7 2020
a. Kẻ \(OH\perp AM ; OK\perp AN\)
Ta có: AM = AN ( gt )
Suy ra: OH = OK ( hai dây bằng nhau cách đều tâm )
Xét hai tam giác OCH và OCK, ta có :
\(\widehat{OHC}=\widehat{OKC}=90^o\)
OC chung
OH = OK (chứng minh trên)
Suy ra: \(\Delta OIH=\Delta OIK\)( cạnh huyền, cạnh góc vuông )
Xét hai tam giác OAH và OBH, ta có :
\(\widehat{OHA}=\widehat{OHB}=90^o\)
OA = OB
OH = OK (chứng minh trên)
Suy ra: \(\Delta OAH=\Delta OBH\)( cạnh huyền, cạnh góc vuông )
\(\widehat{O_3}=\widehat{O_4}\)
Suy ra : \(\widehat{O_1}+\widehat{O_3}=\widehat{O_2}+\widehat{O_4}\)hay \(\widehat{AOC}=\widehat{BOC}\)
Vậy OC là tia phân giác của \(\widehat{AOB}\)
b. Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân )
Suy ra: \(OC\perp AB\)
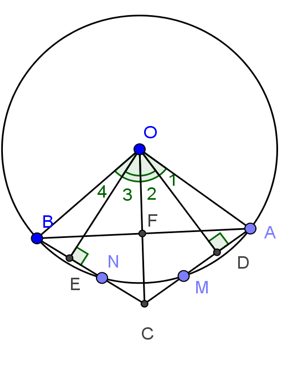
a) Kẻ OP ⊥ AM, OQ ⊥ BN
Ta có: AM = BN (Giả thiết)
Suy ra: OP = OQ (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCP và OCQ, ta có:
Góc OPC= góc OQC=90∘
OC chung
OP = OQ (chứng minh trên)
Suy ra: ∆OCP = ∆OCQ (cạnh huyền, cạnh góc vuông)
Góc O1= góc O2
Xét hai tam giác OAP và OBQ, ta có:
Góc OPA= góc OQB=90∘
OA = OB
OP = OQ ( chứng minh trên)
Suy ra: ∆OAP = ∆OBQ (cạnh huyền, cạnh góc vuông)
Góc O3= Góc O4
Suy ra: Góc O1+góc O3= Góc O2+ góc O4 hay Góc AOC= Góc BOC
Vậy OC là tia phân giác của Góc AOB
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.