Làm dùm e bài 4 với ạ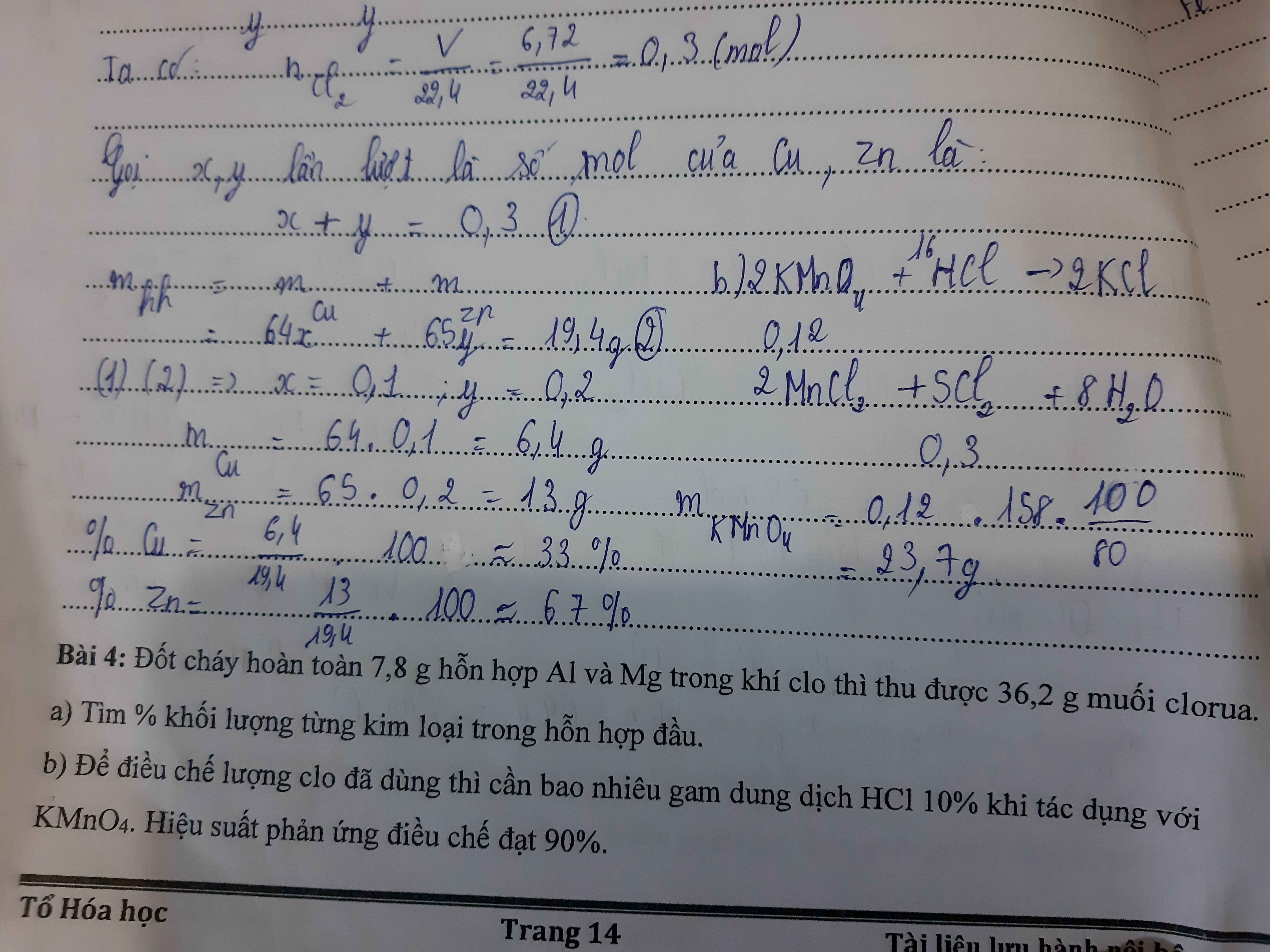
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
27 tháng 2 2022
Câu 2.
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot m\cdot6^2+m\cdot10\cdot0=18m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\Rightarrow h_{max}=\dfrac{18}{10}=1,8m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\Rightarrow z=\dfrac{18}{2g}=\dfrac{18}{2\cdot10}=0,9m\)
c)Cơ năng tại nơi \(W_đ=2W_t\):
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{18}{3\cdot10}=0,6m\)
DT
2
25 tháng 2 2022
Bài 2.
Tóm tắt:
\(v=6\)m/s, \(g=10\)m/s2
a)\(h_{max}=?\)
b)\(W_t=W_đ\Rightarrow z=?\)
c)\(W_đ=2W_t\Rightarrow z'=?\)
Giải chi tiết:
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot6^2=18m\left(J\right)\)
a)Tại nơi có độ cao \(h_{max}\): \(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{18}{g}=\dfrac{18}{10}=1,8m\)
b)Tại nơi thế năng bằng động năng thì cơ năng là
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\)
\(\Rightarrow z=\dfrac{18}{2g}=\dfrac{9}{10}=0,9m\)
c)Tại nơi động năng bằng hai lần thế năng:
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{6}{10}=0,6m\)
25 tháng 2 2022
Bài 3.
a)Cơ năng ban đầu: \(W=W_đ+W_t\)
\(\Rightarrow W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}m\cdot0^2+m\cdot10\cdot20=200m\left(J\right)\)
Cơ năng tại nơi vận tốc vật khi cham đất:
\(W'=\dfrac{1}{2}mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow200m=\dfrac{1}{2}mv'^2\)
\(\Rightarrow v'=20\)m/s
Cách khác nè:Áp dụng công thức( chỉ sử dụng khi tính vận tôc vật chạm đất)
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot20}=20\)m/s
b)Tại nơi có thế năng bằng động năng thì cơ năng là:
\(W_1=W_t+W_đ=2W_t=2mgh\)
Bảo toàn cơ năng: \(W_1=W\)
\(\Rightarrow2mgh=200m\)
\(\Rightarrow h=10m\)
c)Cơ năng tại nơi thế năng gấp 3 động năng:
\(W_2=W_đ+W_t=W_đ+3W_đ=4W_đ=4\cdot\dfrac{1}{2}mv'^2=2mv'^2\)
Bảo toàn cơ năng: \(W_2=W\)
\(\Rightarrow200m=2mv'^2\)
\(\Rightarrow v'=10\)m/s
C1
4
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2022
ĐKXĐ: \(x\ge4\)
\(\sqrt{x+11}\ge\sqrt{x-4}+\sqrt{2x-1}\)
\(\Leftrightarrow x+11\ge3x-5+2\sqrt{\left(x-4\right)\left(2x-1\right)}\)
\(\Leftrightarrow8-x\ge\sqrt{2x^2-9x+4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}8-x\ge0\\\left(8-x\right)^2\ge2x^2-9x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x^2+7x-60\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\-12\le x\le5\end{matrix}\right.\) \(\Rightarrow-12\le x\le5\)
Kết hợp ĐKXD ta được nghiệm của BPT là: \(4\le x\le5\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(x^2-6x+1>\left(2x-3\right)\sqrt{x^2+1}\)
\(\Leftrightarrow\left(x^2+1-9\right)-3\left(2x-3\right)-\left(2x-3\right)\sqrt{x^2+1}>0\)
\(\Leftrightarrow\left(\sqrt{x^2+1}-3\right)\left(\sqrt{x^2+1}+3\right)-\left(2x-3\right)\left(\sqrt{x^2+1}+3\right)>0\)
\(\Leftrightarrow\left(\sqrt{x^2+1}+3\right)\left(\sqrt{x^2+1}-3-\left(2x-3\right)\right)>0\)
\(\Leftrightarrow\sqrt{x^2+1}-2x>0\) (do \(\sqrt{x^2+1}+3>0\) với mọi x)
\(\Leftrightarrow\sqrt{x^2+1}>2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le0\\\left\{{}\begin{matrix}x>0\\x^2+1>4x^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le0\\\left\{{}\begin{matrix}x>0\\-\dfrac{\sqrt{3}}{3}< x< \dfrac{\sqrt{3}}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x< \dfrac{\sqrt{3}}{3}\)
12 tháng 3 2022
Con ko hiểu ngay chỗ khoanh tròn đỏ ạ. Sao thầy ghi là x<=0 , x>0 mà công thức là x<0, x>=0
2 tháng 2
Câu 6:
Tọa độ A là:
\(\left\{{}\begin{matrix}x+5y-7=0\\x+3y-3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+5y=7\\x+3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5y-x-3y=7-3\\x+3y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2\\x=3-3\cdot2=-3\end{matrix}\right.\)
Vậy: A(-3;2)
M(-1;0) là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot x_M\\y_A+y_B=2\cdot y_M\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_B-3=2\cdot\left(-1\right)=-2\\y_B+2=0\end{matrix}\right.\Leftrightarrow B\left(1;-2\right)\)
Phương trình đường cao kẻ từ A xuống BC là x+3y-3=0
=>VTPT là (1;3)
=>BC nhận vecto (-3;1) làm vecto pháp tuyến
Phương trình đường thẳng CB là:
-3(x-1)+1(y+2)=0
=>-3x+3+y+2=0
=>-3x+y+5=0
Gọi N là trung điểm của BC
=>N là giao điểm của hai đường thẳng -3x+y+5=0 và x+5y-7=0
Tọa độ N là:
\(\left\{{}\begin{matrix}-3x+y+5=0\\x+5y-7=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+y=-5\\x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+y=-5\\3x+15y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+y+3x+15y=-5+21\\x+5y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}16y=16\\x=7-5y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=7-5=2\end{matrix}\right.\)
vậy: N(2;1)
Xét ΔABC có
N,M lần lượt là trung điểm của BC,BA
=>NM là đường trung bình
=>NM//AC
N(2;1); M(-1;0)
=>\(\overrightarrow{NM}=\left(-3;-1\right)=\left(3;1\right)\)
=>AC nhận vecto (3;1) làm vecto chỉ phương
=>VTPT là (-1;3)
Phương trình đường thẳng AC là:
-1(x+3)+3(y-2)=0
=>-x-3+3y-6=0
=>-x+3y-9=0
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 2 2022
\(a,Ca+2HCl\rightarrow CaCl_2+H_2\left(1\right)\\ CaO+2HCl\rightarrow CaCl_2+H_2O\left(2\right)\\ Đặt:n_{Ca}=a\left(mol\right);n_{CaO}=b\left(mol\right)\\ \Rightarrow\left\{{}\begin{matrix}111a+111b=22,2\\22,4a=2,24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\\ \Rightarrow\%m_{CaO}=\dfrac{0,1.56}{0,1.56+0,1.40}.100\approx52,83\%\\ \Rightarrow\%m_{Ca}=47,17\%\\ b,n_{HCl}=2.\left(a+b\right)=0,4\left(mol\right)\\ \Rightarrow m_{ddHCl}=\dfrac{0,4.36,5.100}{36,5}=40\left(g\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 2 2022
Bài 30:
\(Đặt:n_{KBr}=a\left(mol\right);n_{NaCl}=b\left(mol\right)\left(a,b>0\right)\\ KBr+AgNO_3\rightarrow AgBr\downarrow+KNO_3\\ NaCl+AgNO_3\rightarrow AgCl\downarrow+NaNO_3\\ \Rightarrow\left\{{}\begin{matrix}119a+58,5b=23,6\\188a+143,5b=47,5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,1\\b=0,2\end{matrix}\right.\\ a,m_{KBr}=0,1.119=11,9\left(g\right)\\ m_{NaCl}=0,2.58,5=11,7\left(g\right)\\ b,n_{AgNO_3}=a+b=0,3\left(mol\right)\\ \Rightarrow V_{ddAgNO_3}=\dfrac{0,3}{0,5}=0,6\left(l\right)=600\left(ml\right)\)
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
Pt bậc 2 có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Leftrightarrow\left(m^2-4\right)m< 0\)
\(\Leftrightarrow m\in\left(-\infty;-2\right)\cup\left(0;2\right)\)
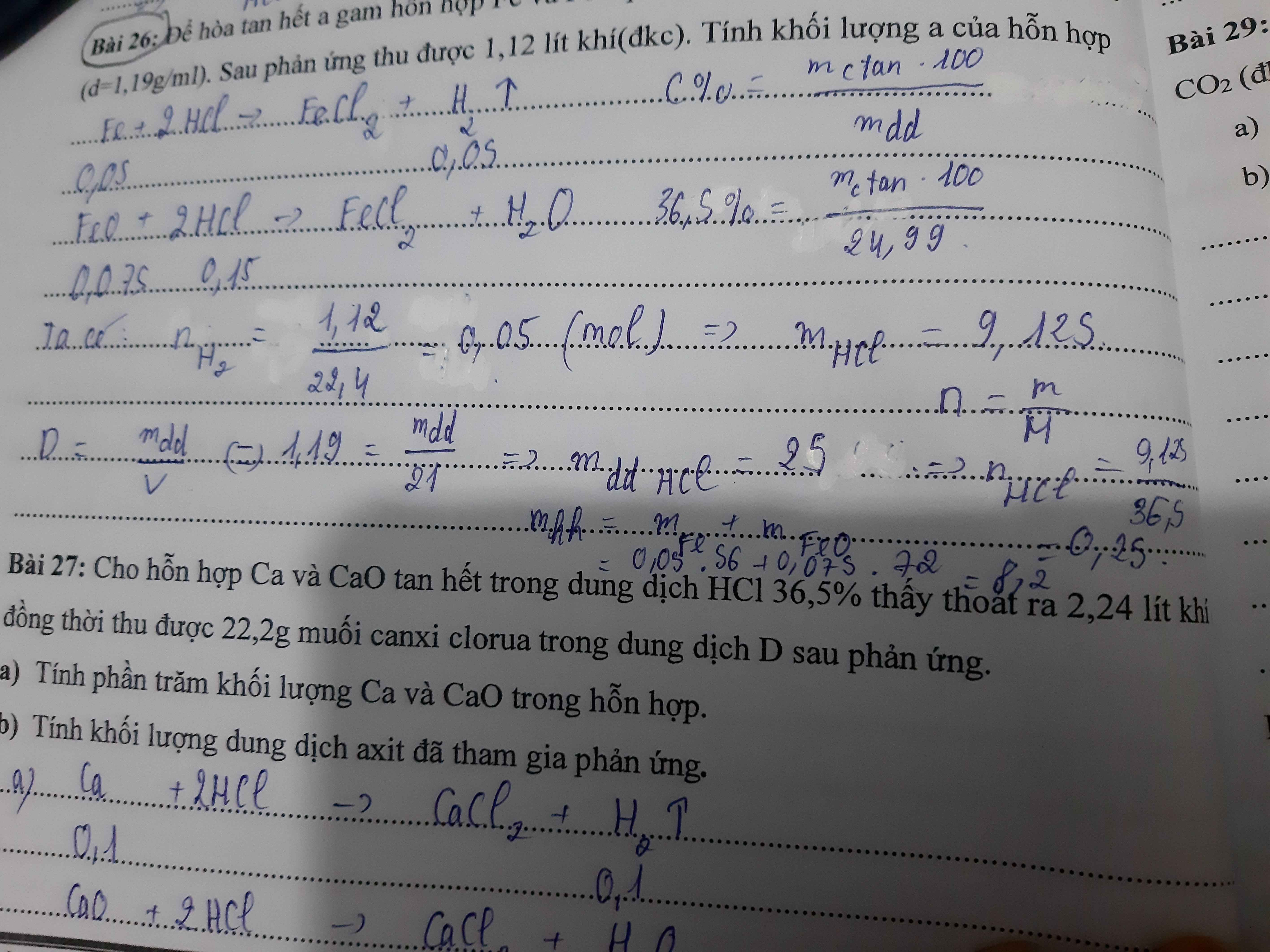
a.Theo định luật bảo toàn khối lượng, ta có:
\(m_{Cl_2}=36,2-7,8=28,4g\)
\(n_{Cl_2}=\dfrac{m}{M}=\dfrac{28,4}{71}=0,4mol\)
\(2Al+3Cl_2\rightarrow\left(t^o\right)2AlCl_3\)
2 3 2 ( mol )
\(2Mg+Cl_2\rightarrow\left(t^o\right)2MgCl_2\)
2 1 2 ( mol )
Gọi \(n_{Al}=x\)
\(n_{Mg}=y\)
\(\Rightarrow m_{Al}=27x\)
\(\Rightarrow m_{Mg}=24y\)
Ta có:
\(\left\{{}\begin{matrix}m_{hh}=27x+24y=7,8\\\dfrac{3}{2}x+\dfrac{1}{2}y=0,4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{75}\\y=\dfrac{1}{25}\end{matrix}\right.\)
\(\Rightarrow m_{Al}=27.\dfrac{19}{75}=6,84g\)
\(\Rightarrow m_{Mg}=24.\dfrac{1}{25}=0,96g\)
\(\%m_{Al}=\dfrac{6,84.100}{7.8}=87,7\%\)
\(\%m_{Mg}=100\%-87,7\%=12,3\%\)