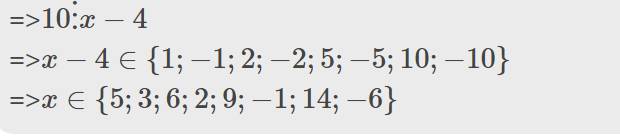M= 51.52.53.54...100 1.3.5.7.99 2) Chứng minh M có giá trị là số tự nhiên M =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em nên ghi đề cụ thể ra em ơi, chứ đề này cô thấy nó chưa đầy đủ. bt là các số tự nhiên là sao em?

Ta có : \(\frac{x}{x+y}>\frac{x}{x+y+z}\)
\(\frac{y}{y+z}>\frac{y}{x+y+z}\)
\(\frac{z}{z+x}>\frac{z}{x+y+z}\)
Cộng theo vế , suy ra : \(M=\frac{x}{x+y}+\frac{y}{y+z}+\frac{z}{z+x}>\frac{x}{x+y+z}+\frac{y}{x+y+z}+\frac{z}{x+y+z}\)
\(< =>M>\frac{x+y+z}{x+y+z}=1\)(*)
Lại có : \(\frac{x}{x+y}< \frac{x+z}{x+y+z}\)
\(\frac{y}{y+z}< \frac{y+x}{y+z+x}\)
\(\frac{z}{z+x}< \frac{z+y}{z+x+y}\)
Cộng theo vế , suy ra : \(M=\frac{x}{x+y}+\frac{y}{y+z}+\frac{z}{z+x}< \frac{x+z}{x+y+z}+\frac{y+x}{x+y+z}+\frac{z+y}{x+y+z}\)
\(< =>M< \frac{2\left(x+y+z\right)}{x+y+z}=2\)(**)
Từ (*) và (**) \(< =>1< M< 2\)
Từ đó ta có điều phải chứng minh

+ \(M=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{2019^2}\)
+ \(\frac{1}{2^2}>0,\frac{1}{3^2}>0,...,\frac{1}{2019^2}>0\)
\(\Rightarrow M>0\) (1)
+ \(M< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+...+\frac{1}{2018\cdot2019}\)
\(\Rightarrow M< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2018}-\frac{1}{2019}\)
\(\Rightarrow M< 1-\frac{1}{2019}< 1\) (2)
+ Từ (1) và (2) => 0 < M < 1
=> M không là số tự nhiên

1: \(D=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{x^2-16}\)
\(=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{x-4+x\left(x+4\right)+24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{-x^2+x+20+x^2+4x}{\left(x+4\right)\left(x-4\right)}=\dfrac{5x+20}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{5\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5}{x-4}\)
2: Khi x=10 thì \(D=\dfrac{5}{10-4}=\dfrac{5}{6}\)
3: \(M=\left(x-2\right)\cdot D=\dfrac{5\left(x-2\right)}{x-4}\)
Để M là số nguyên thì \(5\cdot\left(x-2\right)⋮x-4\)
=>\(5\left(x-4+2\right)⋮x-4\)
=>\(5\left(x-4\right)+10⋮x-4\)
=>\(10⋮x-4\)
=>\(x-4\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{5;3;6;2;9;-1;14;-6\right\}\)

a/ Ta có: `2a = 3b => a/3 = b/2`
Đặt `a/3 = b/2 = k` \(\left(k\ne0\right)\)
`=> a = 3k ; b = 2k`
`=> M =`\(\dfrac{\left(3k\right)^3-2.3k.\left(2k\right)^2+\left(2k\right)^3}{\left(3k\right)^2.2k+3k.\left(2k\right)^2+\left(2k\right)^3}=\dfrac{27k^3-24k^3+8k^3}{18k^3+12k^3+8k^3}=\dfrac{11k^3}{38k^3}=\dfrac{11}{38}\)
Vậy `M = 11/38`.
b/ Giả sử tồn tại số chính phương `a^2` có tổng các số tự nhiên là 20142015
Vì \(20142015⋮3\) nên \(a^2⋮3\)
\(\Rightarrow a^2⋮3^2\)
\(\Rightarrow a^2⋮9\)
Mà \(20142015⋮9̸\Rightarrow a^2⋮9̸\) (vô lí)
`=>` Không tồn tại số chính phương `a^2` nào có tổng các số tự nhiên là 20142015
\(\Rightarrow\) 1 số tự nhiên có tổng các chữ số là `20142015` không phải là số chính phương (đpcm)