cho tam giác ABC cân tại A.Đường cao AH=5,đường cao BD=6.Tính BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tự vẽ hình nha!!!
AH là đường cao của tam giác ABC cân tại A
=> AH là đường trung trực của tam giác ABC.
=> H là trung điểm của BC
=> HB = HC = BC/2 = 6/2 = 3
Tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\) (định lí Pytago)
\(AH^2=AB^2-BH^2\)
\(AH^2=5^2-3^2\)
\(AH^2=25-9\)
\(AH^2=16\)
\(AH=\sqrt{16}\)
\(AH=4\)

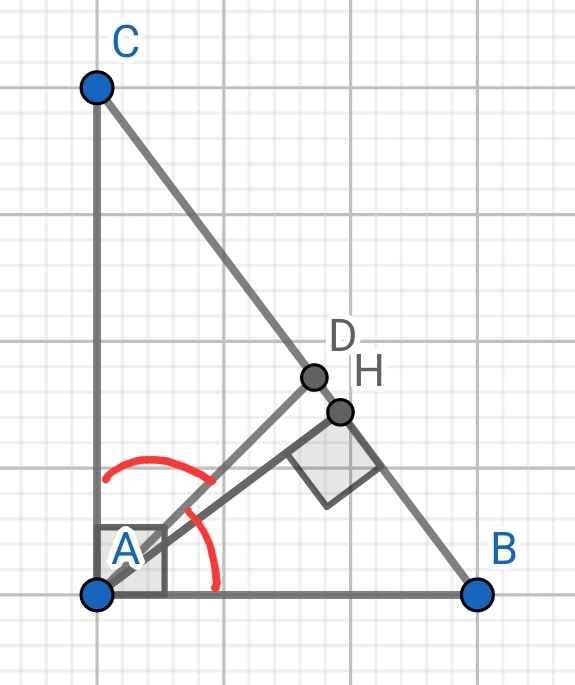
a) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠B = ∠CAH (cùng phụ C)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/HC = HB/AH
⇒ AH.AH = HB.HC
⇒ AH² = HB.HC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC/HC = BC/AC
⇒ AC.AC = HC.BC
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
Do AD là tia phân giác của ∠BAC
⇒ BD/CD = AB/AC
⇒ AB/BD = AC/CD
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AB/BD = AC/CD = (AB + AC)/(BD + CD) = (3 + 4)/5 = 7/5
Do AB/BD = 7/5
⇒ BD = AB.5/7 = 3.5/7 = 15/7 (cm)


Sửa đề: AC=4cm; AB=3cm
a: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=4/8=0,5
=>AD=1,5cm; CD=2,5cm
\(BD=\sqrt{1.5^2+3^2}=\dfrac{3}{2}\sqrt{5}\left(cm\right)\)


a, Xét ΔABC và ΔHBA có :
\(\widehat{A}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔABC vuông tại A, theo định lý Pi-ta-go ta có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có : \(\Delta ABC\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AC}{AH}=\dfrac{BC}{AB}\)
hay \(\dfrac{8}{AH}=\dfrac{10}{6}\)
\(\Rightarrow AH=\dfrac{8.6}{10}=4,8\left(cm\right)\)
c, Xét ΔAHB và ΔCHA có :
\(\widehat{BHA}=\widehat{AHC}=90^0\)
\(\widehat{BAH}=\widehat{C}\left(phụ\cdot với\cdot\widehat{B}\right)\)
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{BH}{AH}\)
\(\Rightarrow AH^2=HC.BH\)
d, Xét ΔABD và ΔHBI có :
\(\widehat{H}=\widehat{A}=90^0\)
\(\widehat{ABD}=\widehat{HBI}\left(phân\cdot giác\cdot BD\right)\)
\(\Rightarrow\Delta ABD\sim\Delta HBI\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BD}{BI}\)
\(\Rightarrow AB.BI=BD.HB\left(đpcm\right)\)

Gợi ý:
Đáp số là 7,5
biết rồi sao phải hỏi