Cho Tam giác ABC nhọn H là trực tâm.CMR:AB+BC+CA>3/2(AH+BH+CH)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
0
17 tháng 8 2019
Bổ đề: Cho đường tròn (O) với 2 dây AX,AY. Gọi Z,T lần lượt là hình chiếu của O trên AX,AY. Biết \(\frac{OZ}{AX}=\frac{OT}{AY}\). Khi đó AX = AY.
Chứng minh bổ đề (Quan sát hình bên trái): Thấy ngay Z và T lần lượt là trung điểm của AX,AY
Kết hợp \(\frac{OZ}{AX}=\frac{OT}{AY}\)suy ra \(\frac{OZ}{AZ}=\frac{OT}{AT}\). Mà ^OZA = ^OTA (=900) nên \(\Delta\)OAZ ~ \(\Delta\)OAT (c.g.c)
=> ^OAZ = ^OAT => 2 tam giác cân tại O: \(\Delta\)AOX và \(\Delta\)AOY bằng nhau => AX = AY.
Giải bài toán: Vẽ (O) ngoại tiếp \(\Delta\)ABC. Gọi M,N,P thứ tự là hình chiếu của O lên BC,CA,AB
Kẻ đường kính CC'. Khi đó AC' // BH (Cùng vuông góc AC), BC' // AH
Do vậy tứ giác AC'BH là hình bình hành => AH = BC' = 2OM (Vì OM là đường trung bình \(\Delta\)CBC')
Tương tự BH = 2ON, CH = 2OP. Từ đó kết hợp với giả thiết \(\frac{AH}{BC}=\frac{BH}{CA}=\frac{CH}{AB}\)
Suy ra \(\frac{OM}{BC}=\frac{ON}{CA}=\frac{OP}{AB}\). Áp dụng Bổ đề ta thu được AB=BC=CA
Vậy nên tam giác ABC là tam giác đều (đpcm).
18 tháng 8 2020
vừa nghĩ được một cách dễ hơn dùng tam giác đồng dạng, ta chứng minh được \(BC.AH=CA.BH=AB.CH\)
\(\frac{AH}{BC}=\frac{BH}{CA}=\frac{CH}{AB}\)\(\Leftrightarrow\)\(\frac{BC.AH}{BC^2}=\frac{CA.BH}{CA^2}=\frac{AB.CH}{AB^2}\)
\(\Leftrightarrow\)\(\frac{1}{BC^2}=\frac{1}{CA^2}=\frac{1}{AB^2}\)
\(\Leftrightarrow\)\(AB=BC=CA\)
8 tháng 8 2018
Tham khảo nha .
Vẽ HD // AC . và HE // AB
Ta có : \(HD//AC\)
và \(BH\perp AC\)( vì H là trực tâm của tam giác ABC )
\(\Rightarrow HD\perp BH\)
\(\Rightarrow DB>BH\)
( Cạnh đối diện với góc vuông)
Chứng minh tương tự như trên ta có :
\(EC//DH\)
\(\Rightarrow CH\perp AB\)
\(\Rightarrow CH\perp CE\)
\(\Rightarrow EC>CH\)(Cạnh đối góc vuông)
Mặt khác ta có :
\(HD//AE\)
\(HE//DA\)
\(\Rightarrow\)Tứ giác AEHD là hình bình hành
\(\Rightarrow AD=HE\)
Xét tam giác AEH có :
\(HE+AE>AH\)
\(\Rightarrow AD+AE>AH\)
\(\Leftrightarrow AB+AC=AD+DB+AE+EC\)
\(=\left(AD+AE\right)+DB+EC>AH+BH+CH\)
Chứng minh tương tự ta có :
\(AB+BC>AH+BH+CH\)
\(AC+BC>AH+BH+CH\)
Do đó : \(2\left(AB+BC+AC\right)>3\left(AH+BH+CH\right)\)
\(\Rightarrow AB+BC+AC>\frac{3}{2}\left(AH+BH+CH\right)\)(đpcm)
11 tháng 10 2023
3:
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
\(\widehat{FCA}\) chung
Do đó: ΔCEH đồng dạng với ΔCFA
=>CE/CF=CH/CA
=>\(CE\cdot CA=CH\cdot CF\)
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
\(\widehat{FCB}\) chung
Do đó: ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>CD*CB=CH*CF=CE*CA
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{EBC}\) chung
Do đó: ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>\(BD\cdot BC=BH\cdot BE\)
Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
góc DBA chung
Do đó: ΔBDA đồng dạng với ΔBFC
=>BD/BF=BA/BC
=>BD*BC=BF*BA
=>BD*BC=BF*BA=BH*BE
\(AH\cdot AD+BH\cdot BE=AF\cdot AB+BF\cdot BA=BA^2\)
\(AH\cdot AD+CH\cdot CF=AE\cdot AC+CE\cdot CA=AC^2\)
\(BH\cdot BE+CH\cdot CF=BD\cdot BC+CD\cdot CB=BC^2\)
Do đó: \(2\left(AH\cdot AD+BH\cdot BE+CH\cdot CF\right)=BA^2+AC^2+BC^2\)
=>\(AH\cdot AD+BH\cdot BE+CH\cdot CF=\dfrac{AB^2+AC^2+BC^2}{2}\)
17 tháng 9 2023
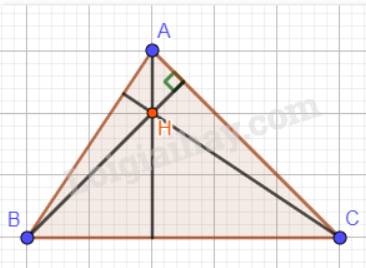
Tam giác ABC có H là trực tâm nên:
a) \(AH \bot BC\);
b) \(BH \bot AC\);
c) \(CH \bot AC\).
LX
0
FF
17 tháng 8 2016
thiếu đề nhưng mk đã làm 1 bài giống thế này nên biết đoạn sau của nó như sau: CMR:AB+BC+CA>3/2(AH+BH+CH)...Nếu ko đúng thì bỏ qua nhé!
Nếu chỉ có BDT đươn thuần thì :
Qua H kẻ đt // AC cắt AB tại X và đt // AB cắt AC tại Y => XHY là hbh và HX vg BH, HY vg CH
AB + AC = BX + (XA + AY) + YC = BX + (AX + XH) + YC > HB + HA + HC
Tương tự có BA + BC > HA + HB + HC, CA + CB > HA + HB + HC
Cộng vế theo vế 3 bđt ta có 2(AB + AC + BC) > 3(HA + HB + HC)
```````````````````````````````````````...
Ta se Cm một BDT mạnh hơn và toàn diện hơn
Giả sử a >=b >= c. Do 2S = a ha = b hb = c hc =>ha <= hb <= hc
Goij A1; B1 ; C1 lan luot la hinh chieu cua A; B : C len cac canh cua Tam giac ABC
Ta co ha = AH.S/( Sb + Sc) ≤ hb = BH.S/(Sa + Sc) => AH( Sa + Sc) ≤ BH( Sb + Sc) (1 )
Ta se CM Sa ≥ Sb
DO Sa/Sb = BC1/AC1 = BC cosB /( AC cosA) = sinA cosB/(sinB cosA) = tanA/tanB ≥ 1 do a ≥ b suy ra Sa≥ Sb => Sa + Sc ≥ Sb + Sc ( 2)
Tu (1) va (2 ) suy ra AH ≤ BH, tuong tu ta suy ra BH ≤ CH do do AH ≤ BH ≤ CH \
Do 6S = a ha + b hb + c hc = aAH + b BH + c CH + 2(Sa+Sb+Sc) =
= aAH + b BH + c CH +2S => aAH + b BH + c CH = 4S
Áp dụng BDT che-bu-sep ta co (a+b+c)(AH + BH + CH) <= 3( a AH + b BH + c CH)
= 12S = 6absinC = 24R^2 sinA sinB sinC
Ta dự đoán 12R^2 sinA sinB sinC <= 1/(2√3) (a+b+c)^2 = 2/(√3)R^2 * ( sinA + sinB + sinC)^2
<=> sinA sinB sinC < = 1/(6√3) ( sinA + sinB + sinC)^2
Ta có (sinA + sinB + sinC )^2 <= 3( sin^2A + sin^2B + sin^2C) =
= 3/2 ( 2 - cos^2C + cosC cos( A-B) ) <= 3/2 ( 2 -cos^2C + cosC)
<= 27/4 =>sinA + sinB + sinC ≤ 3√3/2
=> 3√3/2 ≥ 3³√(sinA sinB sinC) => ³√(sinA sinB sinC) ≤ √3/2
suy ra (sinA + sinB + sinC)²/(sinA sinB sinC) ≥ 9/³√(sinA sinB sinC) ≥ 6√3
Từ đó suy ra (a+b+c)(AH + BH + CH) ≤ √3/3 ( a + b + c )² =>
=> 3/2( AH + BH + CH) ≤ √3/2 (a+b+c) < a + b + c
DG
17 tháng 8 2016
THIẾU ĐỀ NHƯNG MÌNH LÀM BÀI TƯƠNG TỰ GIỐNG BÀI CỦA BẠN NHA !
Nếu chỉ có BDT đươn thuần thì :
Qua H kẻ đt // AC cắt AB tại X và đt // AB cắt AC tại Y => XHY là hbh và HX vg BH, HY vg CH
AB + AC = BX + (XA + AY) + YC = BX + (AX + XH) + YC > HB + HA + HC
Tương tự có BA + BC > HA + HB + HC, CA + CB > HA + HB + HC
Cộng vế theo vế 3 bđt ta có 2(AB + AC + BC) > 3(HA + HB + HC)
```````````````````````````````````````...
Ta se Cm một BDT mạnh hơn và toàn diện hơn
Giả sử a >=b >= c. Do 2S = a ha = b hb = c hc =>ha <= hb <= hc
Goij A1; B1 ; C1 lan luot la hinh chieu cua A; B : C len cac canh cua Tam giac ABC
Ta co ha = AH.S/( Sb + Sc) ≤ hb = BH.S/(Sa + Sc) => AH( Sa + Sc) ≤ BH( Sb + Sc) (1 )
Ta se CM Sa ≥ Sb
DO Sa/Sb = BC1/AC1 = BC cosB /( AC cosA) = sinA cosB/(sinB cosA) = tanA/tanB ≥ 1 do a ≥ b suy ra Sa≥ Sb => Sa + Sc ≥ Sb + Sc ( 2)
Tu (1) va (2 ) suy ra AH ≤ BH, tuong tu ta suy ra BH ≤ CH do do AH ≤ BH ≤ CH \
Do 6S = a ha + b hb + c hc = aAH + b BH + c CH + 2(Sa+Sb+Sc) =
= aAH + b BH + c CH +2S => aAH + b BH + c CH = 4S
Áp dụng BDT che-bu-sep ta co (a+b+c)(AH + BH + CH) <= 3( a AH + b BH + c CH)
= 12S = 6absinC = 24R^2 sinA sinB sinC
Ta dự đoán 12R^2 sinA sinB sinC <= 1/(2√3) (a+b+c)^2 = 2/(√3)R^2 * ( sinA + sinB + sinC)^2
<=> sinA sinB sinC < = 1/(6√3) ( sinA + sinB + sinC)^2
Ta có (sinA + sinB + sinC )^2 <= 3( sin^2A + sin^2B + sin^2C) =
= 3/2 ( 2 - cos^2C + cosC cos( A-B) ) <= 3/2 ( 2 -cos^2C + cosC)
<= 27/4 =>sinA + sinB + sinC ≤ 3√3/2
=> 3√3/2 ≥ 3³√(sinA sinB sinC) => ³√(sinA sinB sinC) ≤ √3/2
suy ra (sinA + sinB + sinC)²/(sinA sinB sinC) ≥ 9/³√(sinA sinB sinC) ≥ 6√3
Từ đó suy ra (a+b+c)(AH + BH + CH) ≤ √3/3 ( a + b + c )² =>
=> 3/2( AH + BH + CH) ≤ √3/2 (a+b+c) < a + b + c
```````````````````````````````````````...
Rõ ràng BDT cuối mà ta cm dc mạnh hơn BDT cần CM