N
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2023
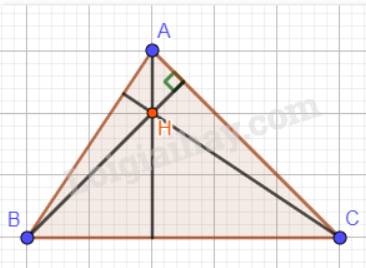
Tam giác ABC có H là trực tâm nên:
a) \(AH \bot BC\);
b) \(BH \bot AC\);
c) \(CH \bot AC\).
LX
0
8 tháng 2 2021
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=CH^2+AH^2\)
hay \(CH^2=AC^2-AH^2\)
Ta có: \(AB^2+CH^2=AH^2+BH^2+AC^2-AH^2\)
nên \(AB^2+CH^2=AC^2+BH^2\)(đpcm)
tham khao
4 tháng 3 2022
b: \(BH=\sqrt{AB^2-AH^2}=5\left(cm\right)\)
BC=BH+CH=5+5=10(cm)
\(AC=\sqrt{12^2+5^2}=13\left(cm\right)\)
b: C=AB+BC+AC=10+13+13=36(cm)
14 tháng 3 2018
Trên tia đối HB lấy D sao cho HD = HB
=> BC - DA
c/m đc :
BC = BD ; góc HBC = góc HBD
=> BD=AD
=> góc DBA = góc DAB = góc BHD ( cùng phụ với góc BCA )
=> góc DBA = góc DAB = góc HBC = góc HBD
Có : góc CDB = góc DBA + góc DAB =góc HBC + góc HBD
=> góc CBD = góc CDB
=> góc CBD = góc CDB = góc BCD = 60 độ
=> góc CAB = 30 độ
Vậy góc BCA = 60 độ và góc CAB = 30 độ
Tk mk nha
14 tháng 4 2022
\(HC=\sqrt{AC^2-AH^2}=16\left(cm\right)\)
BC=BH+HC=21(cm)
\(AB=\sqrt{AH^2+HB^2}=13\left(cm\right)\)
C=AB+BC+AC=13+20+21=54(cm)
14 tháng 4 2022
Xét tam giác vuông AHB có
AH ^2 + BH ^2 = AB ^2 ( Pytago)
=> AB ^2 = 12^2 + 5^2
=> Ab = 13
Xét tam giác vuông AHC có
AH^2 + HC^2 = AC ^2 ( Pytago)
=> HC^2 = AC^2 - AH^2 = 20^2 -12^2
=> HC =16
BC = HC + BH = 16 + 5 = 21
Chu vi tam giác ABC là AB + AC + BC = 13 + 20 + 21= 54 cm