Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn tham khảo nha
Vòi thứ hai chảy đầy bể trong:
(24 - 6) ⋅20/18=20(giờ)
Vòi thứ nhất chảy đầy bể trong:
20-5=15(giờ)
Đáp số: Vòi thứ nhất :15 giờ15 giờ
Vòi thứ hai :20 giờ20 giờ
Nguyễn Hữu Đức Hiếu
Nếu để vòi thứ 2 chảy thì hết thời gian là;
\(\left(24-6\right)\cdot\frac{20}{18}=20\left(giờ\right)\)
Nếu để vòi thứ 1 chảy thì hết thời gian là:
\(20-15=5\left(giờ\right)\)
Đáp số: Vòi thứ 1:\(5giờ\)
Vời thứ 2:\(20giờ\)
\(15p=0,25h;20p=\dfrac{1}{3}h\)
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, vòi 1 chảy được \(\dfrac{1}{x}\)(bể)
Trong 1 giờ, vòi 2 chảy được \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được 3/4(bể)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\left(1\right)\)
Trong 15p=0,25 giờ vòi 1 chảy được:
\(0,25\cdot\dfrac{1}{x}=\dfrac{1}{4}\cdot\dfrac{1}{x}\left(bể\right)\)
Trong 20p=1/3 giờ, vòi 2 chảy được:
\(\dfrac{1}{3}\cdot\dfrac{1}{y}\left(bể\right)\)
Nếu vòi 1 chảy trong 15p và vòi 2 chảy trong 20p thì hai vòi chảy được 5/24 bể nên ta có:
\(\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\\\dfrac{1}{x}\cdot\dfrac{1}{4}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{4}\cdot\dfrac{1}{y}=\dfrac{3}{16}\\\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{4}\cdot\dfrac{1}{y}-\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{3}{16}-\dfrac{5}{24}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{y}\cdot\dfrac{-1}{12}=\dfrac{-1}{48}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{1}{x}=\dfrac{3}{4}-\dfrac{1}{4}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là 2 giờ và 4 giờ
Gọi thời gian chảy 1 mình đầy bề của vòi 1 và vòi 2 lần lượt là x và y giờ (x;y>0)
Trong 1 giờ hai vòi lần lượt chảy được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần bể
Do 2 vòi cùng chảy trong 6h đầy bể nên: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)
Hai vòi chảy 2h và khóa vòi 1, để vòi 2 chảy 12 giờ đầy bể nên: \(2\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+12.\dfrac{1}{y}=1\)
\(\Rightarrow\dfrac{2}{x}+\dfrac{14}{y}=1\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{14}{y}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{9}\\\dfrac{1}{y}=\dfrac{1}{18}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=9\\y=18\end{matrix}\right.\)
Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
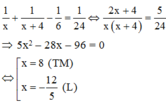
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D
Gọi thời gian chảy riêng của vòi 1 ; vòi 2 chảy đầy bể lần lượt là x;y ( x;y > 0 )
1 giờ vòi 1 chảy riêng được 1/x bể
1 giờ vòi 2 chảy riêng được 1/y bể
2 vòi cùng chảy thì sau 15 giờ thì đầy bể ta có pt :
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\)(1)
Nếu mở 2 vòi trong 6 giờ rồi khóa vòi 1 thì vòi 2 phải chảy 24h nữa thì đầy bể
ta có pt : \(\dfrac{6}{x}+\dfrac{30}{y}=1\)(2)
Từ (1) ; (2) ta có hệ pt \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{6}{x}+\dfrac{30}{y}=1\end{matrix}\right.\)Đặt 1/x = u ; 1/y = v
Ta có hệ \(\left\{{}\begin{matrix}u+v=\dfrac{1}{15}\\6u+30v=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=\dfrac{1}{24}\\v=\dfrac{1}{40}\end{matrix}\right.\)
Theo cách đặt \(\left\{{}\begin{matrix}x=24\\y=40\end{matrix}\right.\)(tm)
Vậy vòi 1 chảy riêng trong 24 giờ thì đẩy bể
vòi 2 chảy riêng trong 40 giờ thì đầy bể
nếu ko có câu hỏi thì bạn ko đăng trống không như này