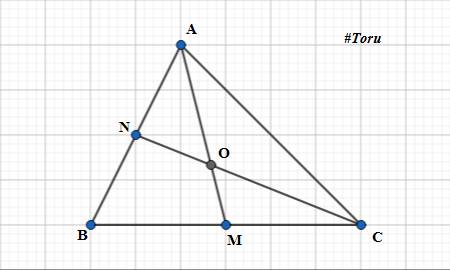
Cho tam giác ABC, trên BC lấy điểm M sao cho BM=MC, trên AB lấy điểm N sao cho AN=NB.Cạnh AM cắt cạnh CN tại D. Tính độ dài cạnh AD biết AM=24cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NX
26 tháng 8 2023
Ta có:
Nối \(B\) với \(O\)
\(S_{OCM}=S_{OMB}\left(BM=MC\right)\) \(\Rightarrow\) chung đường cao hạ từ \(O\)
\(S_{CNB}=S_{ACN}=\left(AN=NB\right)\Rightarrow\) chung đường cao hạ từ \(C\)
\(S_{ONB}=S_{AON}.S_{AON}=\dfrac{1}{2}S_{ABC}-S_{ONMB}.S_{OMC}\)
\(=\dfrac{1}{2}S_{ABC}-S_{ONMB}\)
\(\Rightarrow S_{AON}=S_{OMC};S_{OMC}=\dfrac{1}{6}S_{ABC}\) và \(S_{ACO}\)
Độ dài đoạn \(OA\) là:
\(24.\left(\dfrac{1}{2}+\dfrac{1}{6}\right)=16\left(cm\right)\)
26 tháng 8 2023
ĐÂY LÀ TOÁN LỚP SÁU MÌNH CHỌN NHẦM LỚP MONG CÁC BẠN THÔNG CẢM
TM
8 tháng 7 2017
BM=MC => AM là đường trung tuyến của tam giác ABC
AN=NB => CN là đường trung tuyến của tam giác ABC
AM cắt CN tại O => O là trọng tâm của tam giác ABC => \(AO=\frac{2}{3}AM=\frac{2}{3}.24=16\left(cm\right)\)
DP
8 tháng 7 2017
Nối B với O
SOCM = SOMB (BM = MC ; chung đường cao hạ từ O)
SCNB = SACN (AN = NB ; chung đường cao hạ từ C) .
SONB = SAON . SAON = \(\frac{1}{2}\)SABC - SONMB. SOMC = \(\frac{1}{2}\)SABC - SONMB
=> SAON = SOMC ; SOMC = \(\frac{1}{6}\)SABC và SACO
=> độ dài đoạn OA = \(24\times\left(\frac{1}{2}+\frac{1}{6}\right)=16\left(cm\right)\)
×AB. Trên cạnh BC lấy điểm M sao cho BM bằng 
×BC. AM cắt CN tại O. Tính diện tích BNOM, biết diện tích tam giác OAN bằng 8cm
.
1 tháng 4 2017
Diện tích tam giác ANC = 1/3 diện tích tam giác AMC
vì hai tam giác này có chung chiều cao hạ từ đỉnh C mà đáy AN = 1/3 đáy AM
Diện tích tam giác AMC là :
36 x 3 = 108 ( cm2 )
Diện tích tam giác AMC = 2/3 diện tcihs tam giác ABC
vì 2 tam giác này có chung chiều cao hạ từ đỉnh A mà đáy MC = 2/3 đáy BC
a) Diện tích tam giác ABC là
108 : 2 x3 = 162 ( cm2 )
b) Nối B với N ta có diện tích tam giác BNM = 1/3 diện tích tam giác BNC
Vì hai tam giác này co chung chiều cao hạ từ đỉnh N mà đáy BM= 1/3 đáy BC
Diện tcihs tam giác ANC = 1/3 diện tcihs tam giác BNC
Diện tích tam giác ANC là :
36 x 3 = 108 ( cm2)
Diện tích tam giác ABN là :
162 - ( 108 + 36 ) = 18 ( cm2 )
Ta thấy hai tam giác ANC và BNC có chung cạnh NC mà diện tích tam giác ANC = 1/3 diện tích tam giác BNC
Nên chiều cao hạ từ đỉnh A = 1/3 chiều cao hạ từ đỉnh B ( AH = 1/3 BP)
Diện tích tam giác AKN = 1/3 diện h stam giác BNM
cạnh đáy KN mà chiều cao AH = 1/3 chiều cao BP
Ta thấy hai tam giác AKN và BKN có chung chiều cao hạ từ đỉnh N mà diện tích tam giác AKN = 1/3 diện tích tam giác
BKN nên đáy AK = 1/3 đáy BK vậy AK/BK = 1/3
T
19 tháng 1
Ta có: \(\left\{{}\begin{matrix}BM=MC\left(M\in BC\right)\\AN=NB\left(N\in AB\right)\end{matrix}\right.\left(gt\right)\)
\(\Rightarrow M,N\) lần lượt là các trung điểm của \(BC\) và \(AB\)
\(\Rightarrow AM,CN\) là các đường trung tuyến của \(\Delta ABC\)
Xét \(\Delta ABC\) có:
\(AM,CN\) là các đường trung tuyến
\(AM\cap CN=\left\{O\right\}\)
Do đó: \(O\) là trọng tâm của \(\Delta ABC\) (t/c)
\(\Rightarrow OA=\dfrac{2}{3}AM\) (t/c)
\(\Rightarrow OA=\dfrac{2}{3}\cdot24=16\left(cm\right)\) (vì \(AM=24cm\))
Vậy \(OA=16cm\).
CH
Cô Hoàng Huyền
Admin
VIP
10 tháng 5 2016
Đây là Toán lớp 5 nên ta sẽ dùng diện :)
Ta thấy dt(ANC)=dt(AMC) \(\left(=\frac{dt\left(ABC\right)}{2}\right)\)
Từ đó ta thấy dt(ANO)=dt(MOC).
Do tam giác ANO và BNO chung chiều cao, đấy bằng nhau nên diện tích bằng nhau. tương tự diện tích tam giác MOC và BOM bằng nhau, diện tích ABM bằng diện tích AMC.
Như vậy \(\frac{dt\left(OMC\right)}{dt\left(AMC\right)}=\frac{dt\left(OMC\right)}{dt\left(ABM\right)}=\frac{1}{3}\Rightarrow\frac{dt\left(AOC\right)}{dt\left(AMC\right)}=\frac{2}{3}\Rightarrow\frac{OA}{AM}=\frac{2}{3}\)
Vậy OA = 16 cm.
Have a good time :)
15 tháng 3 2022
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC