cho tam giác MAB có 3 góc nhọn nội tiếp đường tròn O. Vẽ MH vuông gócc với AB tại H, HD vuông góc với AM tại D, HC vuông góc với MB tại C.
1. chứng minh tứ giác MDHC là tứ giác nội tiếp đường tròn
2. chứng minh góc MDC = góc MHB
3. Chứng minh MO vuông góc với CD
Giúp tôi câu 3 mọi người ơi.
Bài 2: Cho tam giác ABC có các góc đều nhọn góc A = 45 độ. Vẽ các đường cao BD và CE của tam giác ABC. Gọi H là giao điển của BD và CE.
1 chứng minh tứ giác AHDE là tứ giác nội tiếp
2. chứng minh HD = DC
3. Tính tỷ số DE/BC
giúp tôi ý 3

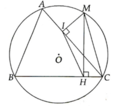
Bài 1. câu 3
Kẻ đường kính MK của (O), cắt CD tại I => góc MAK = 900 (góc nội tiếp chắn nửa (O))
Tam giác AHM vuông tại H có đường cao HD => MH2 = MA.MD
tương tự MH2 = MB.MC => MA.MD = MB.MC => MD/MB = MC/MA và góc AMB chung => tam giác MCD đồng dạng tam giác MAB
=> góc MDC = góc MBA mà góc MBA = góc MKA (cùng chắn cung MA) => góc MDC = góc MKA hay gócMDI = góc MKA
tam giác MDI và tam giác MKA có góc M chung và góc MDI = góc MKA (cmt) nên đồng dạng => góc MIA = MAK = 900
=> MK vuông góc CD hay MO vuông góc CD
Bài 2. câu 3 : Tỉ số \(\frac{DE}{BC}=\frac{1}{\sqrt{2}}\)
chỉ tôi câu 2 bài 1 vs