có thể tìm x là một số nguyên để đa thức 3x^3+x^2+6x-4=2013 được không? . tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 4 2019
a) Ta có : \(C\left(x\right)+B\left(x\right)=A\left(x\right)\)
\(\Leftrightarrow C\left(x\right)=A\left(x\right)-B\left(x\right)\)
\(=x^5+3x^4-2x^3-9x^2+11x-6-\left(x^5+3x^4-2x^3-x-8\right)\)
\(=x^5+3x^4-2x^3-9x^2+11x-6-x^5-3x^4+2x^3+x+8\)
\(=-9x^2+12x+2\)
b) Ta có : \(C\left(x\right)=2x+2\)
\(\Leftrightarrow-9x^2+12x+2=2x+2\)
\(\Leftrightarrow\) \(-9x^2+10x=0\)
\(\Leftrightarrow\) \(x\left(-9x+10\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x=\frac{10}{9}\end{cases}}\)
c) Giả sử : \(C\left(x\right)=2012\)
\(\Leftrightarrow\)\(-9x^2+12x+2=2012\)
\(\Leftrightarrow-9x^2+12x-2010=0\)
\(\Leftrightarrow\)\(9x^2-12x+2010=0\)
\(\Leftrightarrow\left(9x^2-2.3x.2+4\right)+2006=0\)
\(\Leftrightarrow\left(3x-2\right)^2+2006=0\)(vô nghiệm vì \(\left(3x-2\right)^2\ge0\forall x\inℝ\))
Do đó với x nguyên thì C(x) không thể nhận giá trị bằng 2012.
18 tháng 3 2016
Nhẩm nghiệm ta lấy ước của hệ số tự do đem chia cho 1
thay vào rồi thì sẽ biết
H
12 tháng 12 2018
ĐỂ x4 - x3 + 6x2 -x \(⋮x^2-x+5\)
\(\Rightarrow x-5=0\Rightarrow x=5\)
H
12 tháng 12 2018
b , ta có : \(3x^3+10x^2-5⋮3x+1\)
\(\Rightarrow3x^3+x^2+9x^2+3x-3x-1-4⋮3x+1\)
\(\Rightarrow x\left(3x+1\right)+3x\left(3x+1\right)-\left(3x+1\right)-4⋮3x+1\)
mà : \(\left(3x+1\right)\left(4x-1\right)⋮3x+1\)
\(\Rightarrow4⋮3x+1\Rightarrow3x+1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Nếu : 3x + 1 = 1 => x = 0 ( TM )
3x + 1 = -1 => x = -2/3 ( loại )
3x + 1 = 2 => x = 1/3 ( loại )
3x + 1 = -2 => x = -1 ( TM )
3x + 1 = 4 => x = 1 ( TM )
3x + 1 = -1 => x = -5/3 ( loại )
\(\Rightarrow x\in\left\{0;\pm1\right\}\)
K
8 tháng 7 2019
1.Gọi a,b,c là độ dài 3 cạnh tam giác vuông ABC, c là cạnh huyền.
Ta có \(a^2+b^2=c^2;a,b,c\in\)N* , diện tích tam giác ABC là \(S=\frac{ab}{2}\)
Trước hết ta chứng minh ab chia hết cho 12.
+ Chứng minh \(ab⋮3\): Nếu cả a và b đồng thời không chia hết cho 3 thì \(a^2+b^2\)chia 3 dư 2. Suy ra số chính phương \(c^2\)chia 3 dư 2, vô lí.
+ Chứng minh \(ab⋮4\): - Nếu a,b chẵn thì \(ab⋮4\)
- Nếu trong hai số a,b có số lẻ, chẳng hạn a lẻ.
Lúc đó c lẻ. Vì nếu c chẵn thì \(c^2⋮4\), trong lúc \(a^2+b^2\)không thể chia hết cho 4. Đặt \(a=2k+1,c=2h+1,k,h\in N\)
Ta có: \(b^2=\left(2h+1\right)^2-\left(2k+1\right)^2=4\left(h-k\right)\left(h+k+1\right)\)
\(=4\left(h-k\right)\left(h-k+1\right)+8k\left(h-k\right)⋮8\)
Suy ra \(b⋮4\). Nếu ta chia cạnh AB (chẳng hạn) thành 6 phần bằng nhau, nối các điểm chia với C thì tam giác ABC được chia thành 6 tam giác, mỗi tam giác có diện tích bằng \(\frac{ab}{2}\)là một số nguyên.
K
8 tháng 7 2019
2. Với \(a\in Z,\)ta có: \(P\left(a\right)=a^5-3a^4+6a^3-3a^2+9a-6\)
Nếu a chia hết cho 3 thì tất cả các số hạng trong P(a) đều chia hết cho 9, trừ số hạng cho 6, do đó P(a) không chia hết cho 9, nghĩa là \(P\left(a\right)\ne0\).
Nếu a không chia hết cho 3 thì \(a^5\)không chia hết cho 3 trong khi tất cả các số hạng khác trong P(a) đều chia hết cho 3, do đó P(a) không chia hết cho 3, nghĩa là \(P\left(a\right)\ne0\). Vậy \(P\left(a\right)\ne0\)với mọi \(a\in Z\).
18 tháng 11 2017
MK ko biế đúng ko nữa , sai thì ý kiến
a)
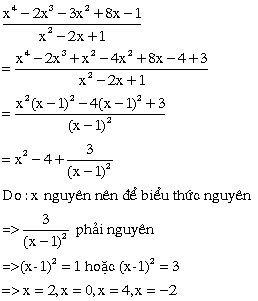
b)
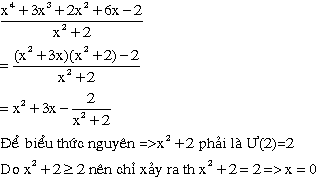
Chúc các bn hok tốt
Tham khảo nhé
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
\(C=\dfrac{\left(x^2+3x\right)\left(x^2+2\right)-2}{x^2+2}=x^2+3x-\dfrac{2}{x^2+2}\)
\(C\in Z\Leftrightarrow2⋮\left(x^2+2\right)\)
\(\Leftrightarrow x^2+2=2\Rightarrow x=0\)