giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
Chắc là biến đổi trong bài tìm pt mặt phẳng
Từ hệ 2 pt đầu ta rút ra được: \(\left\{{}\begin{matrix}c=-a-b\\d=2a+b\end{matrix}\right.\)
Thế vào pt cuối:
\(\dfrac{\left|3a-b\right|}{\sqrt{a^2+b^2+\left(a+b\right)^2}}=\dfrac{3}{\sqrt{2}}\)
\(\Rightarrow2\left(3a-b\right)^2=9\left(a^2+b^2\right)+9\left(a+b\right)^2\)
\(\Rightarrow15ab+8b^2=0\Rightarrow\left[{}\begin{matrix}b=0\\b=-\dfrac{15a}{8}\end{matrix}\right.\)
TL
2
16 tháng 11 2021
Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.
10 tháng 7 2021
\(A=\left(t+2\right)\left(3t-1\right)-t\left(3t+3\right)-2t+7\)
\(=3t^2-t+6t-2-3t^2-3t-2t+7\)
\(=\left(3t^2-3t^2\right)-\left(t-6t+3t+2t\right)-\left(2-7\right)\)
\(=0-0-\left(-5\right)=5\)
HV
10 tháng 7 2021
A=(t+2)(3t−1)−t(3t+3)−2t+7A=(t+2)(3t−1)−t(3t+3)−2t+7
=3t2−t+6t−2−3t2−3t−2t+7=3t2−t+6t−2−3t2−3t−2t+7
=(3t2−3t2)−(t−6t+3t+2t)−(2−7)=(3t2−3t2)−(t−6t+3t+2t)−(2−7)
=0−0−(−5)=5
NT
0
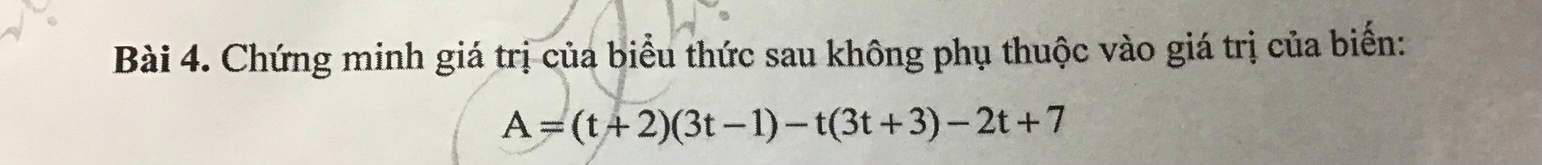
Bài 10:
\(\Leftrightarrow n^2-4n+6n-24+18⋮n-4\)
\(\Leftrightarrow n-4\inƯ\left(18\right)\)
\(\Leftrightarrow n-4\in\left\{-3;-2;-1;1;2;3;6;9;18\right\}\)
hay \(n\in\left\{1;2;3;5;6;7;10;13;22\right\}\)
Bài 1:
Vì \(a,b,c\) là 3 số tự nhiên nhỏ nhất khác 0 thỏa mãn: \(64a=80b=96c\)
=>\(64a=80b=96c=BCNN\left(64;80;96\right)\)
\(64=2^6\) ; \(80=2^4.5\) ; \(96=2^5.3\)
=>\(BCNN\left(64;80;96\right)=2^6.3.5=960\)
=>\(64a=80b=96c=960\)
=>\(a=\dfrac{960}{64}=15\) ; \(b=\dfrac{960}{80}=12\) ; \(c=\dfrac{960}{96}=10\) (đều thỏa mãn điều kiện)
Bài 2:
-Vì \(n⋮3\) nên \(n=3k\) (\(k\in N\))
=>\(n^3+n^2+3=\left(3k\right)^3+\left(3k\right)^2+3=27k^3+9k^2+3=3\left(9k^3+3k^2+1\right)\)
-Do \(9k^3⋮9\) ; \(\left(3k^2+1\right)\)không chia hết cho 9 (\(3k^2+1\) chia 9 dư 1;4;7).
=>\(3\left(9k^3+3k^2+1\right)\) không chia hết cho 9.
-Vậy với \(n\in N,n⋮3\) thì \(n^3+n^2+1\) không chia hết cho 9.
Bài 3:
\(A=1+4+4^2+...+4^{2016}\)
\(4A=4+4^2+4^3+...+4^{2017}\)
\(4A-A=4+4^2+4^3+...+4^{2017}-\left(1+4+4^2+...+4^{2016}\right)\)
\(3A=4^{2017}-1\)
\(A=\dfrac{4^{2017}-1}{3}\)
=>\(B-A=\dfrac{4^{2017}}{3}-\dfrac{4^{2017}-1}{3}=\dfrac{1}{3}\)