cho hình bình hành ABCD. Từ B kẻ các đường thẳng BE vuông góc CD và BK vuông góc AD. Biết KE=3a, BD=5a. Tính khoảng cách từ B đến trực tâm tam giác BEK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 3 2021
(xin lỗi vì mình không biết chèn hình, các bạn chịu khó tự vẽ. Cảm ơn ạ)
Gọi O là giao điểm 2 đường chéo
I là trung điểm BK
H là trung điểm BE
Xét tam giác(tg) BKD có
I là trung điểm BK
O là trung điểm BD
=>OI là đường trung bình của tgBKD
=> OI // KD
=> OI \(\perp\)BK
Lại có I là trung điểm BK
=> O \(\in\)đường trung trực của BK
*Tương tự ta sẽ chứng minh được O \(\in\)đường trung trực của BE
Từ đó suy ra O là trực tâm của tgBKE
Ta có BO = BD:2
<=> BO = \(\frac{5}{2}\)
Vậy...
Done~
CM
23 tháng 3 2017
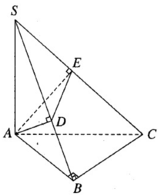
Gọi d là khoảng cách từ E đến mặt phẳng (SAB)
Ta có:
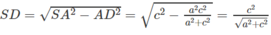
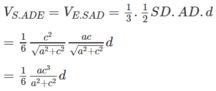
Kết hợp với kết quả trong câu a)
ta suy ra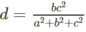 
I
22 tháng 4 2020
gọi M là trung điểm của AF . Ta có OM là đường trung bình của tam giác ACF
\(=>OM//CF,OM=\frac{1}{2}CF\)
ta lại có \(OM//CF,CF\perp CD\left(gt\right)\)
\(=>OM\perp CD.Mà\left(AB//CD\right)\)
\(=>OM//BE\)(1)
mặt khác OM , AM là 2 đường cao của tam giác ABO
=> M là trực tâm của tam giác ABO
=>\(BM\perp AC.Mà\left(EO\perp AC\right)=>BM//EO\left(2\right)\)
từ 1 zà 2 => tứ giác BMOE là hbh => OM=BE
ta có
\(OM=BE;OM=\frac{1}{2}CF=>BE=\frac{1}{2}CF\left(and\right)BE//OM//CF\)
\(\Delta KCF\)có \(CF//BE=>\frac{KE}{KF}=\frac{BE}{CF}=\frac{1}{2}\)