Cho a,b là 2 số dương thỏa mãn a+b=1 . Chứng minh \(\left(1+\frac{1}{a}\right)\left(1+\frac{1}{b}\right)\ge\)9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: \(\frac{a}{\left(a+1\right)\left(b+1\right)}+\frac{b}{\left(b+1\right)\left(c+1\right)}+\frac{c}{\left(c+1\right)\left(a+1\right)}.\)
\(\ge3\sqrt[3]{\frac{a.b.c}{\left(a+1\right)^2.\left(b+1\right)^2.\left(c+1\right)^2}}=\frac{3}{\sqrt[3]{\left(a+1\right)^2.\left(b+1\right)^2.\left(c+1\right)^2}}\) (vì abc=1) (*)
Mặt khác: \(\left(a+1\right)^2.\left(b+1\right)^2.\left(c+1\right)^2\ge64abc=64=4^3\) (vì abc=1)
=> \(\sqrt[3]{\left(a+1\right)^2.\left(b+1\right)^2.\left(c+1\right)^2}\ge4\) (**)
Từ (*), (**)=> đpcm
Bạn dưới kia làm ngược dấu thì phải,mà bài này hình như là mũ 3
\(\frac{a^3}{\left(a+1\right)\left(b+1\right)}+\frac{a+1}{8}+\frac{b+1}{8}\ge3\sqrt[3]{\frac{a^3\left(a+1\right)\left(b+1\right)}{64\left(a+1\right)\left(b+1\right)}}=\frac{3a}{4}\)
Tương tự rồi cộng lại:
\(RHS+\frac{2\left(a+b+c\right)+6}{8}\ge\frac{3\left(a+b+c\right)}{4}\)
\(\Leftrightarrow RHS\ge\frac{3}{4}\) tại a=b=c=1

\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
Bất đẳng thức trên
<=> 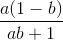 + 1 +
+ 1 + 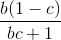 + 1 +
+ 1 + 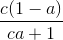 + 1 ≥ 3
+ 1 ≥ 3
<=> 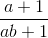 +
+ 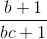 +
+ 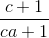 ≥ 3 (*)
≥ 3 (*)
Ta có: VT(*) ≥ 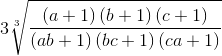
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3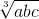 =>
=> 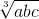 ≤ 1 => abc ≤ 1
≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.

\(abc=1\Rightarrow\left(abc\right)^2=a^2b^2c^2=1\Rightarrow a^2=\frac{1}{b^2c^2}\Rightarrow\frac{1}{a^3\left(b+c\right)}=\frac{b^2c^2}{a\left(b+c\right)}=\frac{\left(bc\right)^2}{ab+ac}\)
Chứng minh tương tự ta có: \(\frac{1}{b^3\left(c+a\right)}=\frac{\left(ca\right)^2}{bc+ba};\frac{1}{c^3\left(a+b\right)}=\frac{\left(ab\right)^2}{ca+cb}\)
=> \(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}=\frac{\left(ab\right)^2}{bc+ca}+\frac{\left(bc\right)^2}{ab+ca}+\frac{\left(ca\right)^2}{ab+bc}\)
Áp dụng bđt Cauchy-Schwarz dạng Engel: \(\frac{\left(ab\right)^2}{bc+ca}+\frac{\left(bc\right)^2}{ab+ca}+\frac{\left(ca\right)^2}{ab+bc}\ge\frac{\left(ab+bc+ca\right)^2}{bc+ca+ab+ca+ab+bc}=\frac{ab+bc+ca}{2}\)
Tiếp tục áp dụng bđt Cauchy với 3 số dương ta được: \(\frac{ab+bc+ca}{2}\ge\frac{3\sqrt[3]{ab.bc.ca}}{2}=\frac{3\sqrt[3]{\left(abc\right)^2}}{2}=\frac{3\sqrt[3]{1}}{2}=\frac{3}{2}\)
=> \(\frac{\left(ab\right)^2}{bc+ca}+\frac{\left(bc\right)^2}{ab+ca}+\frac{\left(ca\right)^2}{ab+bc}\ge\frac{ab+bc+ca}{2}\ge\frac{3}{2}\)

Đặt \(\left(\frac{1}{a};\frac{1}{b};\frac{1}{c}\right)=xyz\) thì bài toán trở thành
Cho \(x+y+z=xyz\) chứng minh
\(P=xyz+\frac{x^2y^2z^2}{\left(x+y\right)\left(y+z\right)\left(z+x\right)}\ge\frac{9\sqrt{3}}{3}\)
Ta có:
\(t=x+y+z=xyz\le\frac{\left(x+y+z\right)^3}{27}=\frac{t^3}{27}\)
\(\Leftrightarrow t\ge3\sqrt{3}\)
Ta lại có:
\(P\ge\left(x+y+z\right)+\frac{\left(x+y+z\right)^2}{\frac{8\left(x+y+z\right)^3}{27}}=t+\frac{27}{8t}\)
\(=\left(t+\frac{27}{t}\right)-\frac{189}{8t}\ge6\sqrt{3}-\frac{189}{8.3\sqrt{3}}=\frac{27\sqrt{3}}{8}\)
PS: Đề sai rồi nha.

(
hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhh
hhhhhhhhhhhhh

ta có:\(\frac{1}{a^3\left(b+c\right)}+\frac{1}{b^3\left(c+a\right)}+\frac{1}{c^3\left(a+b\right)}\)
=\(\frac{\frac{1}{a^2}}{a\left(b+c\right)}+\frac{\frac{1}{b^2}}{b\left(a+c\right)}+\frac{\frac{1}{c^2}}{c\left(a+b\right)}\)
>= \(\frac{\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)^2}{a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)}\)(BĐT Svaxo)=\(\frac{\left(\frac{ab+bc+ca}{abc}\right)^2}{2\left(ab+bc+ca\right)}=\frac{ab+bc+ca}{2}\)
>= \(\frac{3\sqrt[3]{a^2b^2c^2}}{2}\left(BĐTAM-GM\right)=\frac{3}{2}\)(đpcm)
dấu = khi a=b=c=1
\(\left(1+\frac{1}{a}\right)\cdot\left(1+\frac{1}{b}\right)=\left(1+\frac{a+b}{a}\right)\cdot\left(1+\frac{a+b}{b}\right)\)
= \(\left(2+\frac{b}{a}\right)\cdot\left(2+\frac{a}{b}\right)\)
= \(4+2\cdot\left(\frac{a}{b}+\frac{b}{a}\right)+\frac{a}{b}\cdot\frac{b}{a}=4+2\cdot\left(\frac{a}{b}+\frac{b}{a}\right)+1\)
Mặt khác \(\frac{a}{b}+\frac{b}{a}\ge2\cdot\sqrt{\frac{a}{b}\cdot\frac{b}{a}}=2\)(bất đẳng thức cô-si
từ đó suy ra điều phải chứng minh
Bai nay hinh nhu sai de vi a,b la 2 so nguyen duong nen a+b lon hon hoac bang 2