Cho \(\Delta\)\(ABC\) cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Chứng minh:
a) \(\Delta\)\(ADE\) cân
b) ED // BC
(Vẽ hình và làm hết giùm mk cái)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
29 tháng 1 2022
- Gợi ý:
Câu 1:
a) - Sửa lại đề: Tam giác ABD=Tam giác ICE (c-g-c) do có AB=AC=CI, góc ABC=góc ACB=góc ECI, BD=CE.
b) Do tam giác ABD=Tam giác ICE nên AD=IE :
AE+EI>AI=2AC=AB+AC
=>AE+AD>AB+AC.
Câu 2:
- Tam giác MBD=Tam giác NCE do góc MDB=góc CEN=900, BD=CE,
góc MBD=góc NCE. nên BM=CN
Câu 3:
- AB=AM+BM ; CI=CN+NI.
=>AM=NI.
=>AM+AN=AM+NI=AI=AB+AC.
-c/m MN>BC (c/m mệt lắm nên mình nói ngắn gọn).
MN cắt BC tại F =>MF>DF, NF>EF
MF+NF>DF+EF=DF+CF+CE=DF+CF+BD=BC =>MN>BC
2 tháng 1 2023
a: Xét ΔADE và ΔABC có
góc ADE=góc ABC
góc DAE=góc BAC
Do đó: ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
=>DE//BC
b: Xét ΔAEB và ΔADC có
AE=AD
góc EAB=góc DAC
AB=AC
Do đó: ΔAEB=ΔADC
=>BE=CD
D
19 tháng 1 2022
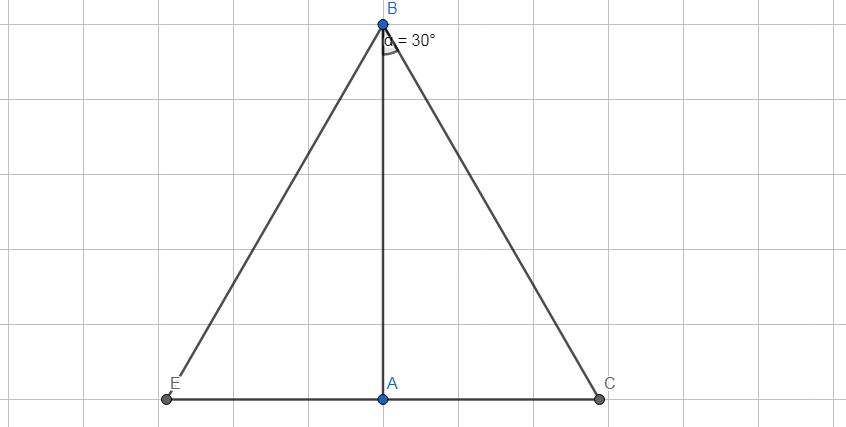
a) Xét tam giác ABC vuông tại A có:
\(\widehat{ABC}+\widehat{ACB}=90^0\)(phụ nhau)
=>300+\(\widehat{ACB}\)=900
=>\(\widehat{ACB}\)=600
Xét tam giác BEC có:
BA là đường cao (BA vuông góc với EC tại A)
BA là trung tuyến (A là trung điểm EC)
=>Tam giác BEC cân tại B mà \(\stackrel\frown{BCE}=60^0\)(cmt)
=>Tam giác BEC đều.
27 tháng 7 2023
a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE
14 tháng 4 2021
1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có
AB=AD(gt)
AC=AE(gt)
Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)
Suy ra: BC=DE(hai cạnh tương ứng)
14 tháng 4 2021
2) Xét ΔABD có AB=AD(gt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)
nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)
bn tự vẽ nha :
a, Xét \(\Delta ADE\)
có \(AD=AE\left(gt\right)\)
\(\Rightarrow\Delta ADE\) là tam giác cân
b, Xét \(\Delta ABC\) và \(\Delta ADE\) có :
\(AB=AD\left(gt\right)\)
\(\widehat{BAC}=\widehat{DAE}\) ( đối đỉnh )
\(AC=AE\left(gt\right)\)
\(\Rightarrow\Delta ABC=\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow\widehat{EDA}=\widehat{ACB}\) ( hai góc tương ứng)
\(\Rightarrow ED\)//\(BC\)
bn có thể trình bày rõ hơn ở phần a đc ko?