Cho đường tròn (O, r) đường kính Bc. Lấy dây AD = R, dây AC và BD cắt nhau tại E. Tìm số đo cung nhỏ AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2021
cho đường tròn O bán kính R đường kính BC,Vẽ dây AD=R,dây AC và dây BD kéo dài cắt nhau tại E
a) tính số đo cung nhỏ CD
b)gọi H là giao điểm của AC và CD.Chứng minh tứ giác ADEH nội tiếp
em cần gấp ạ
19 tháng 3 2021
a) Xét ΔOCD có OC=OD(=R)
nên ΔOCD cân tại O(Định nghĩa tam giác cân)
Xét ΔOCD cân tại O có CD=OC(=R)
nên ΔOCD đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{COD}=60^0\)
hay \(sđ\stackrel\frown{CD}=60^0\)
CM
19 tháng 10 2019
a, Khi M ở ngoài hay M nằm trong đường tròn thì ∆MCD và ∆MBA đều có 2 góc bằng nhau => ĐPCM
Tỷ số đồng dạng là: C D A B = 1 2
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3
CM
23 tháng 4 2017
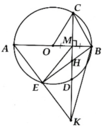
a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3
11 tháng 5 2023
goc ACB=góc AMB=1/2*180=90 độ
=>AM vuông góc BE, BC vuông góc AE
góc ECH+góc EMH=180 độ
=>ECHM nội tiếp
Xet ΔEAB có
AM,BC là đường cao
AM căt BC tại H
=>H là trực tâm
=>EH vuông góc AB
Chưa đủ dữ kiện để tính sđc AC nhỏ bạn nhé. Bạn xem lại đề.