cho chóp SABCD đáy là hình bình hành M thuộc SA , mặt phẳng P qua m song song với SB và AC .tìm thiết diện mặt phẳng P với hình chóp
Mọi người giúp mình bài này với mình cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

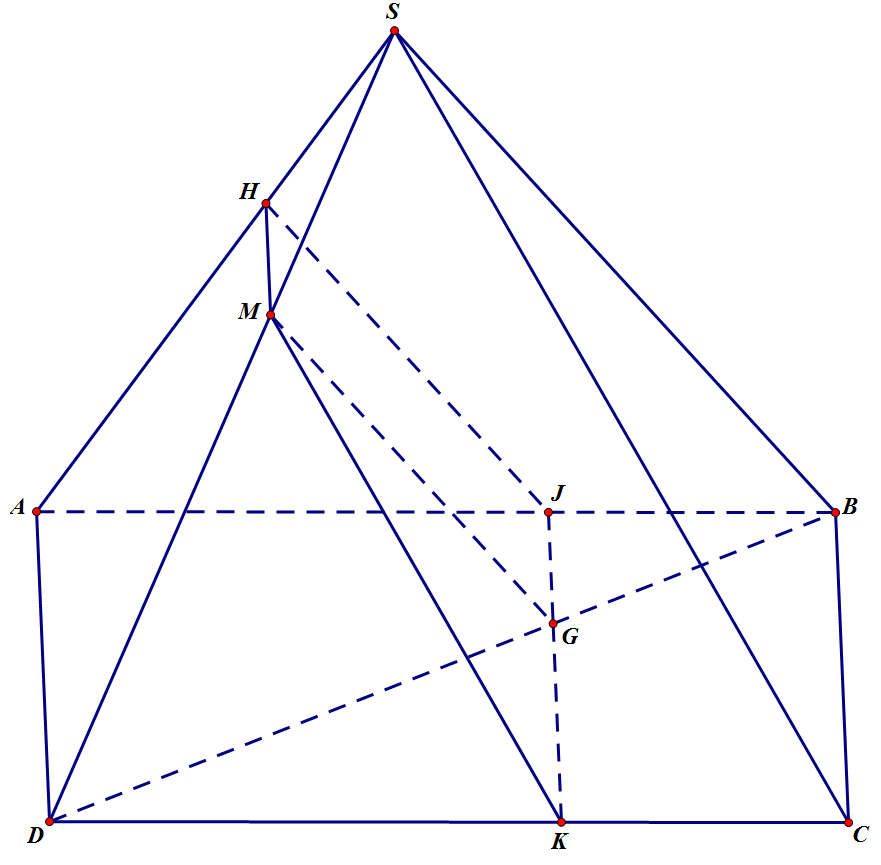
(α) và (SAD) cùng chứa điểm M. Mà (α) // AD nên (α) \(\cap\) (SAD) = d1 với d1 là đường thẳng đi qua M và song song với AD.
Trong (SAD) gọi H = d1 \(\cap\) SA ⇒ (SAD) \(\cap\) (α) = MH
(α) và (SBD) cùng chứa điểm M. Mà (α) // SB nên (α) \(\cap\) (SBD) = d2 với d2 là đường thẳng đi qua M và song song với SB.
Trong (SBD) gọi G = d2 \(\cap\) BD ⇒ (SAD) \(\cap\) (α) = MG
(SAB) và (α) cùng chứa điểm H. Mà (SAB) chứa SB, (α) chứa MG và ta lại có MG // SB
⇒ (SAB) \(\cap\) (α) = d3 với d3 là đường thẳng đi qua H và song song với SB và MG
Trong (SAB) gọi J = \(d_3\cap AB\) ⇒ (SAB) \(\cap\) (α) = HJ
Trong (ABCD) gọi K = JG \(\cap\) CD
Thiết diện cần tìm là tứ giác HMKJ (hình thang hai đáy HM, JK)
*Lưu ý : (α) không cắt (SBC) vì (α) // (SBC).
\(\cap\)

Chắc là mp (P) đi qua A'
Đặt \(V_{SABCD}=V\)
Theo định lý Talet: \(\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{SD'}{SD}=\dfrac{3}{4}\)
Ta có: \(\dfrac{V_{SA'B'C'D'}}{V_{SABCD}}=\dfrac{2V_{SA'B'C'}}{2V_{SABC}}=\dfrac{V_{SA'B'C'}}{V_{SABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}=\dfrac{3}{4}.\dfrac{3}{4}.\dfrac{3}{4}=\dfrac{27}{64}\)
Tỉ số thể tích 2 phần (phần trên chia phần dưới) là: \(\dfrac{27}{64}:\left(1-\dfrac{27}{64}\right)=\dfrac{27}{37}\)

Đáp án D
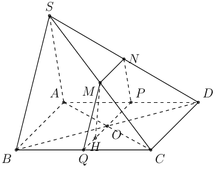
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .
Trong mp (SAB), qua M kẻ đường thẳng song song SB cắt AB tại G \(\Rightarrow G\in\left(P\right)\)
Trong mp (SAC), qua M kẻ đường thẳng song song AC cắt SC tại E \(\Rightarrow E\in\left(P\right)\)
Trong mp (ABCD), qua G kẻ đường thẳng song song AC, lần lượt cắt BC tại F và AD kéo dài tại H
\(\Rightarrow F;H\in\left(P\right)\)
Trong mp (SAD), nối HM kéo dài cắt SD tại I
\(\Rightarrow\) Ngũ giác EFGMI là thiết diện của (P) và chóp