Một vật nặng 4,0 kg được gắn vào một dây thừng dài 2 m. Nếu vật đó quay tự do thành một vòng tròn quanh trục thẳng đứng gắn với đầu dây thì sức căng của dây là bao nhiêu khi căng tối đa và vật có vận tốc 5 m/s? (Giải giúp mình với, mình cần gấp ạ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
14 tháng 5 2018
Đáp án D
Lực căng dây đóng vai trò là lực hướng tâm.
T max = F h t = m v 2 R = 4.5 2 2 = 50 N
24 tháng 11 2021
Lực căng dây cũng giống như lực hướng tâm.
\(T_{max}=F_{ht}=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot4\cdot5^2=50N\)
VT
31 tháng 7 2019
Nếu dây cáp chịu được lực căng tối đa T m a x = 6000 N > 4920 N, thì ở cùng độ cao nêu trên vật có thể đạt được vận tốc tối đa v m a x sao cho :
m v m a x 2 /2 + mgh = T m a x h
VT
26 tháng 7 2017
Độ biến dạng tại vị trí cân bằng của dây là
Chia dao động của vật làm 3 giai đoạn được biểu diễn như hình vẽ
Đáp án B
VT
24 tháng 8 2017
Đáp án B
Độ biến dạng tại vị trí cân bằng của dây là
Chia dao động của vật làm 3 giai đoạn được biểu diễn như hình vẽ
QT
Quoc Tran Anh Le
Giáo viên
16 tháng 12 2023
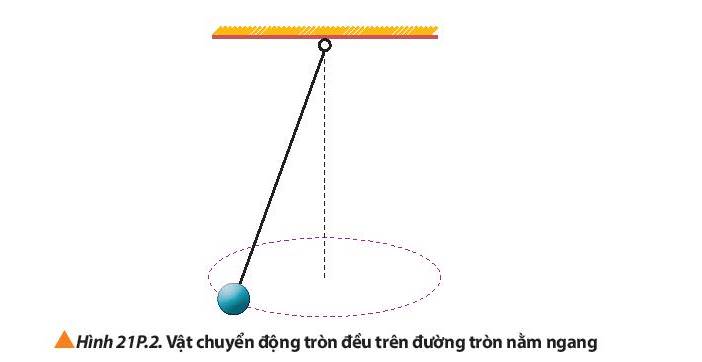
Lực đóng vai trò là lực hướng tâm trong trường hợp trên là lực căng.
=> Vận tốc cực đại của vật để dây không bị đứt là:
\(\begin{array}{l}{T_{\max }} = {F_{ht\max }} = m.\frac{{v_{\max }^2}}{R}\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.R}}{m}} = \sqrt {\frac{{50.1,5}}{{0,5}}} \approx 12,23(m/s)\end{array}\)
VT
24 tháng 4 2019
a.Ta có ω = 2 π f = 2 π .2 = 4 π r a d / s
Khi vật quay tròn đều F d h = F q t l t ⇒ k . Δ l = m . r . ω 2
Mà r = l 0 + Δ l ⇒ k . Δ l = m . l 0 + Δ l . ω 2 ⇒ 12 , 5. Δ l = 0 , 01. 0 , 2 + Δ l . 4 π 2
⇒ Δ l = 0 , 03 m = 3 c m
b. Theo bài ra r max = l max = 0 , 4 m
⇒ F d h ≥ F q t l t ⇒ k . Δ l ≥ m . r . ω 2 ⇒ ω ≤ k . Δ l m . r
Mà Δ l = l 1 − l 0 = 40 − 20 = 20 c m = 0 , 2 m
⇒ ω ≤ 12 , 5.0 , 2 0 , 01.0 , 4 = 25 r a d / s Vậy n = 25.60 2. π = 238 , 73 ( vòng/ phút )
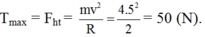
TK:
Gia tốc hướng tâm của vật là \(a_{ht}=\dfrac{v^2}{r}=\dfrac{5^2}{2}=12,5(m/s^2)\)
Khi đó lực hướng tâm tác dụng vào vật là \(F_{ht}=ma_{ht}=4.12,5=50(N)\)