So sánh: 1 + 2 + 22+ 23+ ........+ 250 và 5. 249
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 11 2023
a, A = 1 + 3 + 32 + 33 + ... + 32000
3.A = 3 + 32 + 33+ 33+... + 32001
3A - A = 3 + 32 + 33 + ... + 32001 - (1 + 3 + 32 + 33 + ... + 32000)
2A = 3 + 32 + 33 + ... + 32001 - 1 - 3 - 32 - 33 - ... - 32000
2A = 32001 - 1
A = \(\dfrac{3^{2001}-1}{2}\)
VT
7 tháng 4 2017
1/2 và 5/4
1/2<1
5/4>1
\(\Rightarrow\)1/2 < 5/4
1/3 Và 4/9
1/3 = 3/9
Vì 3/9< 4/9 nên 1/3 < 4/95
3/4 = 15/20
7/10= 14/20
Vì 15/20 > 14/20 nên 3/4 > 7/10
22/23 Và 22/33
22/23 và 22/33 có tử chung là 22 mà 23<33\(\Rightarrow\)22/23>22/33
10/9 và 10/7
10/9 và 10/7 có tử chung là 10 mà 9 >3\(\Rightarrow\)10/7 > 10/9
10/3 và 10/7
10/3 và 10/7 có tử chung là 10 mà 3 < \(\Rightarrow\)10/3 > 10/7
tk mình nha !
7 tháng 4 2017
1/2 < 5/4 , 1/3 < 4/9 , 3/4 > 7/10 , 22/23 = 22/23 , 22/23 < 10/9 , 10/3 > 10/7
VT
5
LN
10 tháng 9 2023
S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)2�−�=(2+22+23+...+210)−(1+2+22+...+29)
\(S=2^{10}-1=2^2.2^8-1=4.2^8-1
HT
LN
11 tháng 9 2023
S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)2�−�=(2+22+23+...+210)−(1+2+22+...+29)
\(S=2^{10}-1=2^2.2^8-1=4.2^8-1
XS
1
19 tháng 9 2015
\(27^{11}=3^{33};81^8=3^{32}\)
\(27^{11}>81^8\)
\(5^{23}=5.5^{22}<6.5^{22}\)
\(7.2^{13}<2^{16}=2^3.2^{13}=8.2^{13}\)
6 tháng 7 2016
thưa BGH olm 24h , cháu làm như vậy có đúng không ạ ;
Ta có : 5^23=5^22+1=5.5^22
Vì : 5.5^22<6.5^22
Nên : 5^23<6.5^22
4 tháng 10 2021
a) 2711 và 818
\(27^{11}=\left(3^3\right)^{11}=3^{3.11}=3^{33}\)
\(81^8=\left(3^4\right)^8=3^{4.8}=3^{32}\)
Vì 333 > 332 ⇒ 2711 >818
b) 523 và 6 . 522
\(5^{23}=5^{22}.5\)
Vì 522 . 5 < 6 . 522 ⇒ 523 < 6 . 522
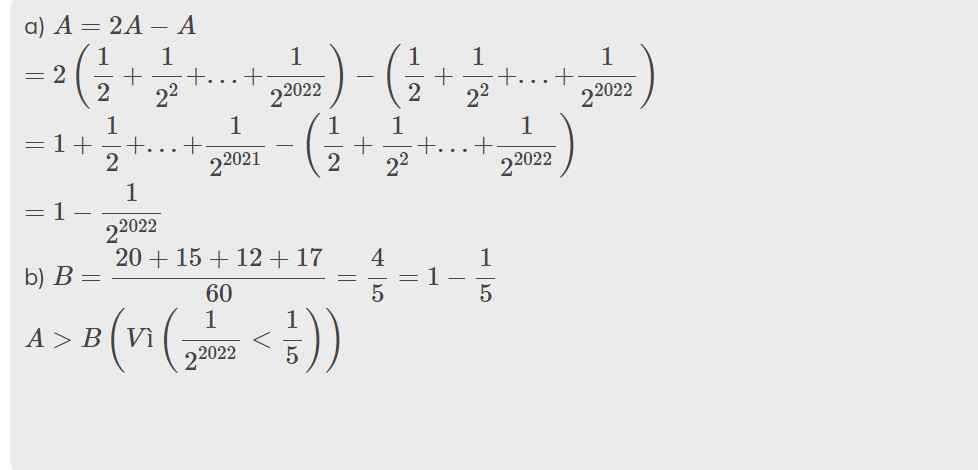
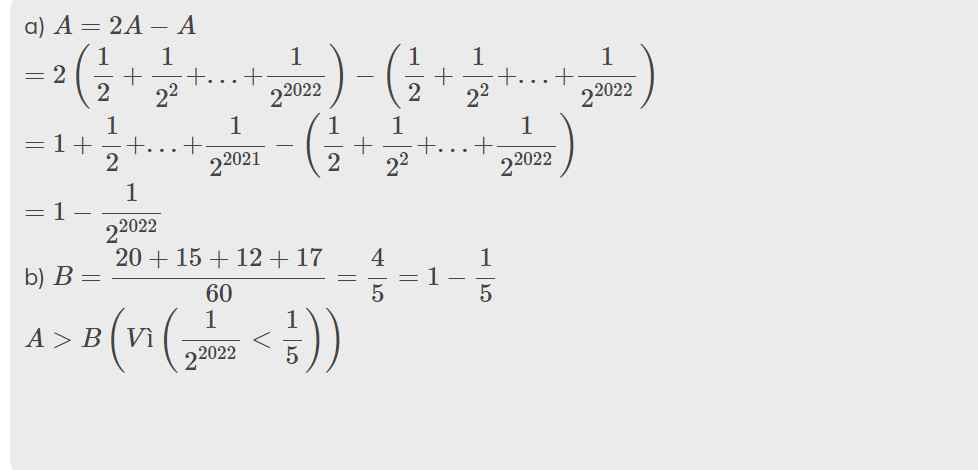
Ta có:
Đặt A=1+2+2^2+....+2^50
A.2 =2+2^2+2^3+.........+2^51
A.2-A=2^51-1
A=2^51-1
Ta thấy: 2^51-1=2^49.2^2-1=2^49.4-1<5.2^49