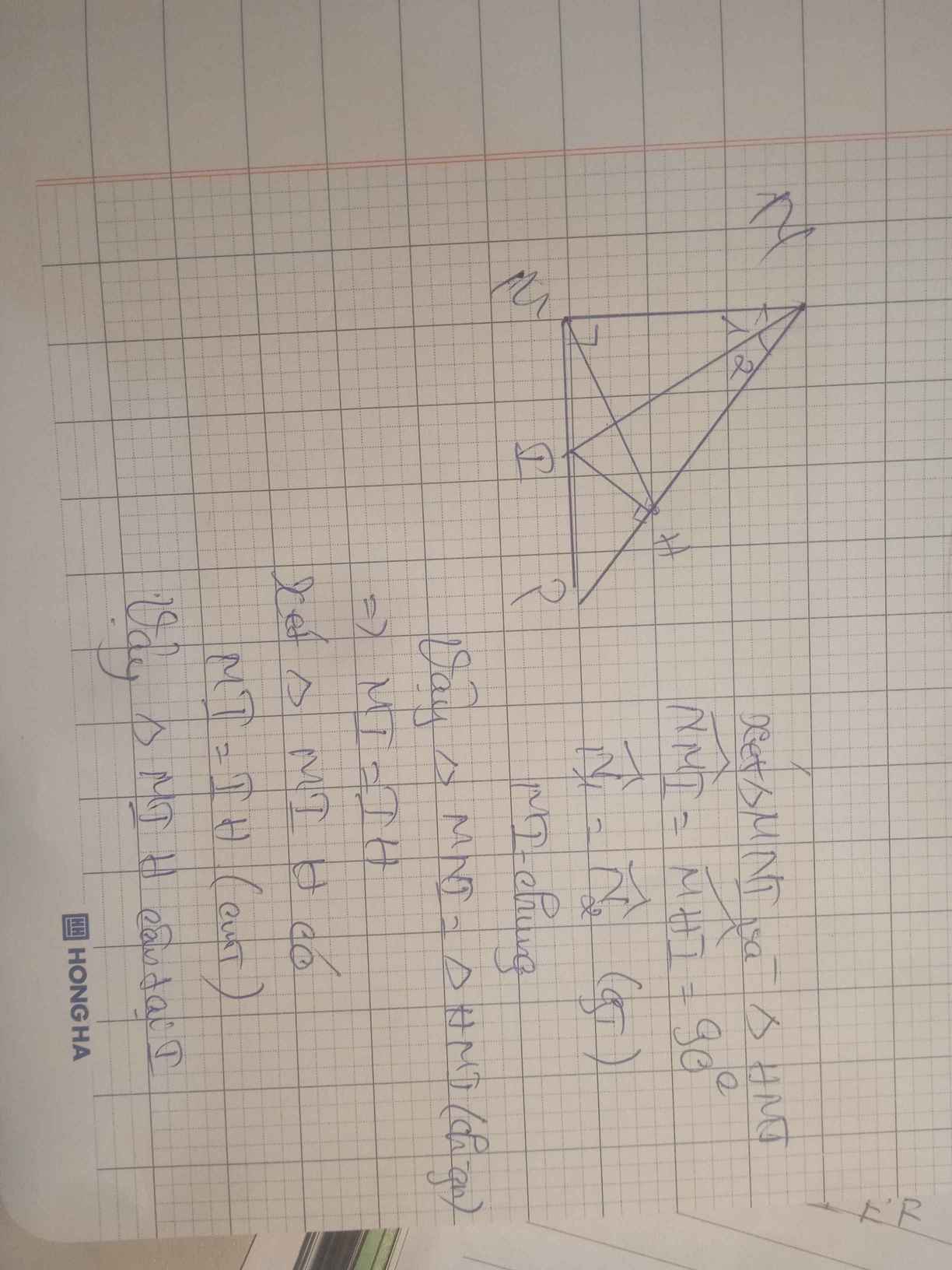
Cho tam giác MNP có: góc M=90 độ,NI là tia phân giác.Gọi H là hình chiếu của I trên NP
a) chứng minh: tam giác MNI=tam giác HNI
b) So sánh MI,IP
c)Gọi HI cắt NM tại O
C/m: tam giác QNP cân
d)Tam giac MNP cần thêm điều kiên gì cách dêu 3 canh của tam giác QNP