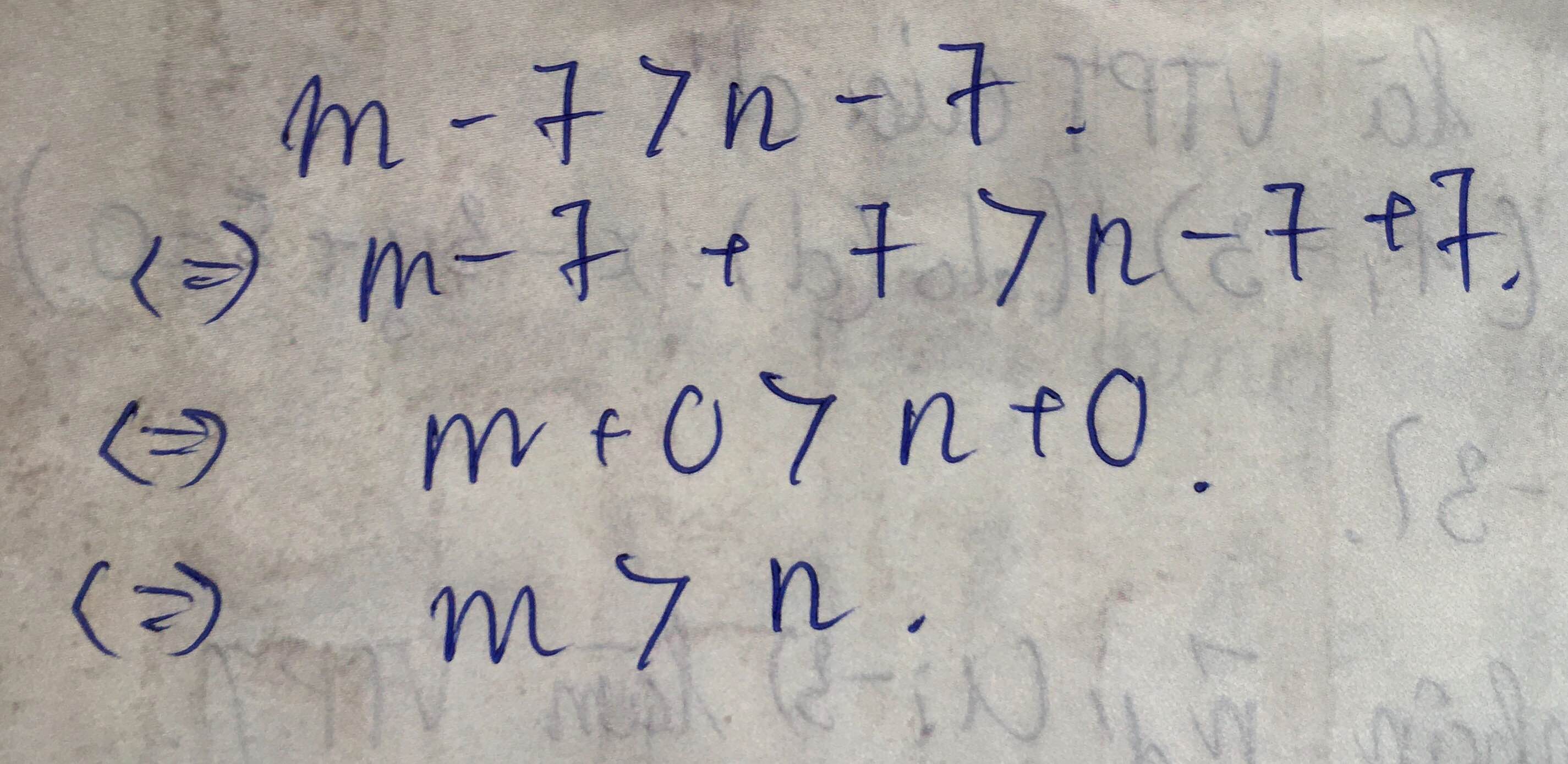so sánh M và N biết : M=ab,52+195,6 N= 1a5,c7 + 9b,6 - 1,c nhanh lên jum
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2019
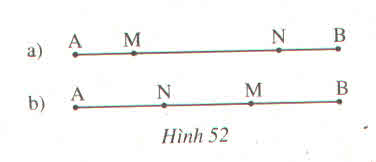
Chúng ta sẽ giải bài toán theo hai trường hợp như trong hình:
Trường hợp a)
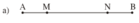
Vì M nằm giữa hai điểm A và N nên AN = AM + MN
Vì N nằm giữa hai điểm B và M nên BM = BN + MN
Theo đề bài: AN = BM nên AM + MN = BN + MN ⇒ AM = BN
(áp dụng tính chất: a + b = c + b ⇒ a = c)
Trường hợp b)
Vì N nằm giữa hai điểm A và M nên AN + MN = AM ⇒ AN = AM - MN
Vì M nằm giữa hai điểm B và N nên BM + MN = BN ⇒ BM = BN - MN
Theo đề bài: AN = BM nên AN - MN = BN - MN ⇒ AM = BN
(áp dụng tính chất: a - b = c - b ⇒ a = c)
Tóm lại: trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau
PT
2
26 tháng 7 2021
ta có: M=10^2020 +1 / 10^2019 +1
=> M/10= 10^2020 +1 / 10( 10^2019 +1 )
= 10^2020+1/ 10^2020 +10
=> 10/A= 10^2020 +10/10^2020 +1
=(10^2020 +1) +9/ 10^2020+1
=10^2020+1 /10^2020+1 + 9/10^2020+1
=1+ 9/10^2020+1
ta lại có: N=10^2021 +1/10^2020 +1
=> N/10= 10^2021+1/ 10(10^2020+1)
= 10^2021+1 / 10^2021+10
=> 10/N=10^2021+10 / 10^2021+1
=(10^2021+1) +9/10^2021+1
=10^2021+1/10^2021+1 +9/10^2021+1
=1+ 9/10^2021+1
ta thấy: 10/M>10N
=>M<N
26 tháng 7 2021
\(M=\dfrac{10^{2020}+1}{10^{2019}+1}=1-\dfrac{9}{10^{2019}+1}\)
\(N=\dfrac{10^{2021}+1}{10^{2020}+1}=1-\dfrac{9}{10^{2020}+1}\)
Ta có: \(10^{2019}+1< 10^{2020}+1\)
\(\Leftrightarrow\dfrac{9}{10^{2019}+1}>\dfrac{9}{10^{2020}+1}\)
\(\Leftrightarrow-\dfrac{9}{10^{2019}+1}< -\dfrac{9}{10^{2020}+1}\)
\(\Leftrightarrow M< N\)
NM
1
8 tháng 7 2016
Ta có:
\(\frac{1}{2}< \frac{2}{3}\)
\(\frac{3}{4}< \frac{4}{5}\)
\(\frac{5}{6}< \frac{6}{7}\)
\(...\)
\(\frac{99}{100}< \frac{100}{101}\)
\(\Rightarrow\frac{1}{2}.\frac{3}{4}.\frac{5}{6}...\frac{99}{100}< \frac{2}{3}.\frac{4}{5}.\frac{6}{7}...\frac{100}{101}\)
\(\Rightarrow M< N\)
24 tháng 4 2021
Giải:
a)Ta có:
C=1957/2007=1957+50-50/2007
=2007-50/2007
=2007/2007-50/2007
=1-50/2007
D=1935/1985=1935+50-50/1985
=1985-50/1985
=1985/1985-50/1985
=1-50/1985
Vì 50/2007<50/1985 nên -50/2007>-50/1985
⇒C>D
b)Ta có:
A=20162016+2/20162016-1
A=20162016-1+3/20162016-1
A=20162016-1/20162016-1+3/20162016-1
A=1+3/20162016-1
Tương tự: B=20162016/20162016-3
B=1+3/20162016-3
Vì 20162016-1>20162016-3 nên 3/20162016-1<3/20162016-3
⇒A<B
Chúc bạn học tốt!
25 tháng 4 2021
Làm tiếp:
c)Ta có:
M=102018+1/102019+1
10M=10.(102018+1)/202019+1
10M=102019+10/102019+1
10M=102019+1+9/102019+1
10M=102019+1/102019+1 + 9/102019+1
10M=1+9/102019+1
Tương tự:
N=102019+1/102020+1
10N=1+9/102020+1
Vì 9/102019+1>9/102020+1 nên 10M>10N
⇒M>N
Chúc bạn học tốt!
18 tháng 4 2017
Giải: Xét cả hai trường hợp sau:
a) Xét trường hợp điểm M nằm giữa hai điểm A và N; Điểm N nằm giữa hai điểm B và M.
- Vì M nằm giữa A và M nên AN= AM+MN (1)
- Vi N nằm giữa B và M nên BM= BN + MN (2)
Mà AN= BM (đề bài) nên từ (1) và (2) suy ra AM + MN = BN + MN
Do đó: AM = BN.
b) Xét trường hợp điểm N nằm giữa A và M; điẻm M nằm giữa B và N.
- Vì N nằm giữa A và M nên AN + NM= AM (3)
- Vì M nằm giữa B và N nên BM + MN= BN(4)
Mà AN=BM(Đề bài) nên từ (3) và(4) AM=BN
VT
10 tháng 11 2017
Chúng ta sẽ giải bài toán theo hai trường hợp như trong hình:
Trường hợp a)
Vì M nằm giữa hai điểm A và N nên AN = AM + MN
Vì N nằm giữa hai điểm B và M nên BM = BN + MN
Theo đề bài: AN = BM nên AM + MN = BN + MN => AM = BN
(áp dụng tính chất: a + b = c + b => a = c)
Trường hợp b)
Vì N nằm giữa hai điểm A và M nên AN + MN = AM => AN = AM - MN
Vì M nằm giữa hai điểm B và N nên BM + MN = BN => BM = BN - MN
Theo đề bài: AN = BM nên AM - MN = BN - MN => AM = BN
(áp dụng tính chất: a - b = c - b => a = c)
Tóm lại: trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau.
CH
Cô Hoàng Huyền
Admin
VIP
8 tháng 1 2018
Bài 1: Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuyết Mai - Toán lớp 6 - Học toán với OnlineMath