giải phương trình
I8-xI=x2+x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2023
a: Δ=(2m-2)^2-4*(-2m)
=4m^2-8m+4+8m=4m^2+4>0
=>Phương trình luôn có hai ngiệm phân biệt
b: x1+x2=2m-2; x1x2=-2m
PT
1
CM
11 tháng 4 2019
Ta có: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
⇔ x 4 + 2 x 2 – x + 1 - 15 x 2 + x + 35 = 0
⇔ x 4 – 13 x 2 + 36 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 13 x 2 + 36 = 0 ⇔ m 2 – 13m + 36 = 0
∆ = - 13 2 – 4.1.36 = 169 – 144 = 25 > 0
∆ = 25 = 5
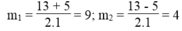
Ta có: x 2 = 9 ⇒ x = ± 3
x 2 = 4 ⇒ x = ± 2
Vậy phương trình đã cho có 4 nghiệm: x 1 = 3; x 2 = -3; x 3 = 2; x 4 = -2
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
Lời giải:
a.
$x^2-x=y^2-1$
$\Leftrightarrow x^2-x+1=y^2$
$\Leftrightarrow 4x^2-4x+4=4y^2$
$\Leftrightarrow (2x-1)^2+3=(2y)^2$
$\Leftrightarrow 3=(2y)^2-(2x-1)^2=(2y-2x+1)(2y+2x-1)$
Đến đây xét các TH:
TH1: $2y-2x+1=1; 2y+2x-1=3$
TH2: $2y-2x+1=-1; 2y+2x-1=-3$
TH3: $2y-2x+1=3; 2y+2x-1=1$
TH4: $2y-2x+1=-3; 2y+2x-1=-1$
b.
$x^2+12x=y^2$
$\Leftrightarrow (x+6)^2=y^2+36$
$\Leftrightarrow 36=(x+6)^2-y^2=(x+6-y)(x+6+y)$
Đến đây xét trường hợp tương tự phần a.
c.
$x^2+xy-2y-x-5=0$
$\Leftrightarrow x^2+xy=x+2y+5$
$\Leftrightarrow 4x^2+4xy=4x+8y+20$
$\Leftrightarrow (2x+y)^2=4x+8y+20+y^2$
$\Leftrightarrow (2x+y)^2-2(2x+y)+1=y^2+6y+21$
$\Leftrightarrow (2x+y-1)^2=(y+3)^2+12$
$\Leftrightarrow (2x+y-1)^2-(y+3)^2=12$
$\Leftrightarrow (2x+y-1-y-3)(2x+y-1+y+3)=12$
$\Leftrightarrow (2x-4)(2x+2y+2)=12$
$\Leftrightarrow (x-2)(x+y+1)=3$
Đến đây đơn giản rồi.
8 tháng 8 2021
a) \(x^2-x=y^2-1\)
\(\Rightarrow x^2-x+1=y^2\)
\(\Rightarrow4x^2-4x+4=4y^2\)
\(\Rightarrow4x^2-4x+1+3=\left(2y\right)^2\)
\(\Rightarrow\left(2x+1\right)^2-\left(2y\right)^2=-3\)
\(\Rightarrow\left(2x-2y+1\right)\left(2x+2y+1\right)=-3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}\left(2x-2y+1\right)\left(2x+2y+1\right)\in Z\\\left(2x-2y+1\right)\left(2x+2y+1\right)\inƯ\left(7\right)\end{matrix}\right.\)
Ta có bảng:
| x-y | -1 | 0 | -2 | 1 |
| x+y | 1 | -2 | 0 | -1 |
| x | 0 | -1 | -1 | 0 |
| y | 1 | -1 | -1 | -1 |
Vậy \(\left(x,y\right)\in\left\{\left(0;1\right);\left(-1;-1\right);\left(-1;-1\right);\left(0;-1\right)\right\}\)
CB
1
AH
Akai Haruma
Giáo viên
12 tháng 2 2023
Lời giải:
Đặt $x^2+x=a$ thì pt trở thành:
$(a-2)(a-3)=12$
$\Leftrightarrow a^2-5a+6=12$
$\Leftrightarrow a^2-5a-6=0$
$\Leftrightarrow (a+1)(a-6)=0$
$\Leftrightarrow a+1=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+1=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+1=0$
$\Leftrightarrow (x+\frac{1}{2})^2=-\frac{3}{4}<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
PT
1
PT
1
CM
9 tháng 12 2017
( x + 1 ) 2 ( x 2 + 4 ) = x 2 − x − 2 (1)
Điều kiện: x2 + 4 ≥ 0 (luôn đùng ∀ x)
( 1 ) ⇔ ( x + 1 ) 2 ( x 2 + 4 ) = ( x − 2 ) ( x + 1 ) ⇔ ( x + 1 ) 2 ( x 2 + 4 ) − ( x − 2 ) = 0 ⇔ x = − 1 2 ( x 2 + 4 ) = x − 2 ( 2 )
Có ( 2 ) ⇔ x ≥ 2 2 ( x 2 + 4 ) = x - 2 2 ⇔ x ≥ 2 x 2 + 4 x + 4 = 0 ⇔ x ≥ 2 x = − 2 (loại)
Vậy tập nghiệm của phương trình đã cho là {–1}
CM
10 tháng 1 2017
(x3 + x2) + (x2 + x) = 0
⇔x2 (x + 1) + x(x + 1) = 0
⇔(x2 + x)(x + 1) = 0
⇔x(x + 1)(x + 1) = 0
⇔x = 0 hoặc x + 1 = 0
⇔x = 0 hoặc x = -1
Vậy tập nghiệm của phương trình là : S = {0; -1}
Chia làm hai trường hợp như vừa nãy:
+ TH1 8-x>=0 thì x=2
+TH2 8-x<0 thì pt vô nghiệm
Vậy pt có nghiệm duy nhất là x=2 k cho mk