giải pt ax2+bx+c=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình ax^2+bx+c=0(a≠0) thỏa mãn điều kiện a+b+c=0 thì có 1 nghiệm x1=1, nghiệm kia x2=c/a
Bước 1. Biến đổi phương trình về đúng dạng \(ax^2+bx+c=0\)
Bước 2. Nếu hệ số a chứa tham số, ta xét 2 trường hợp:
- Trường hợp 1: a = 0, ta giải và biện luận ax + b = 0.
- Trường hợp 2: a ≠ 0. Ta lập Δ = b2 - 4ac. Khi đó:
+ Nếu Δ > 0 thì phương trình có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-b-\sqrt{\Delta}}{2a}\\x_2=\dfrac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\)
+ Nếu Δ = 0 thì phương trình có 1 nghiệm (kép): \(x=\dfrac{-b}{2a}\)
+ Nếu Δ < 0 thì phương trình vô nghiệm.
Bước 3. Kết luận.
Lưu ý:
- Phương trình \(ax^2+bx+c=0\) có nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right..hoặc.\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\end{matrix}\right.\)
- Phương trình \(ax^2+bx+c=0\) có nghiệm duy nhất \(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b\ne0\end{matrix}\right..hoặc.\left\{{}\begin{matrix}a\ne0\\\Delta=0\end{matrix}\right.\)

Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x

\(ax^2+bx+c=0\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=\dfrac{-b}{a}\\P=x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
Ta có pt bậc 2 có 2 nghiệm là \(\dfrac{1}{x^2_1};\dfrac{1}{x^2_2}\)
\(\Rightarrow\left\{{}\begin{matrix}S'=\dfrac{1}{x^2_1}+\dfrac{1}{x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x^2_1x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(\dfrac{-b}{a}\right)^2-\dfrac{2c}{a}}{\left(\dfrac{c}{a}\right)^2}\\P'=\dfrac{1}{\left(\dfrac{c}{a}\right)^2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2}{a^2}-\dfrac{2c}{a}}{\dfrac{c^2}{a^2}}\\P'=\dfrac{1}{\dfrac{c^2}{a^2}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2-2ca}{a^2}}{\dfrac{c^2}{a^2}}=\dfrac{b^2-2ca}{c^2}\\P'=\dfrac{a^2}{c^2}\end{matrix}\right.\)
Theo định lý Viet đảo pt bậc 2 cần lập
\(\Leftrightarrow z^2-S'z+P'=0\)
\(\Leftrightarrow z^2-\dfrac{b^2-2ca}{c^2}z+\dfrac{a^2}{c^2}=0\)

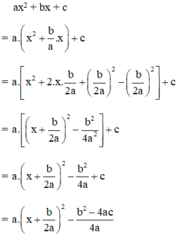
Ta có: a > 0 (gt), 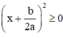 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 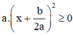
Phương trình ax2 + bx + c = 0 vô nghiệm nên
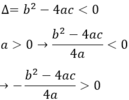
Vậy
a
x
2
+
b
x
+
c
= 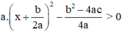 với mọi x.
với mọi x.

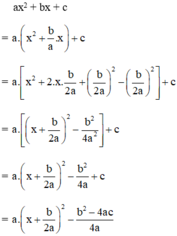
Ta có: a > 0 (gt), 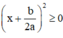 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 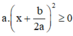
Phương trình ax2 + bx + c = 0 vô nghiệm nên
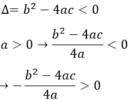
Vậy ax2 + bx + c = 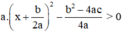 với mọi x.
với mọi x.

#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
\(\text{Δ}=b^2-4ac\)
Nếu Δ>0 thì phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-b-\sqrt{\text{Δ}}}{2a}\\x_2=\dfrac{-b+\sqrt{\text{Δ}}}{2a}\end{matrix}\right.\)
Nếu Δ=0 thì phương trình có nghiệm kép là x=-b/2a
Nếu Δ<0 thì phương trình vô nghiệm