Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: D
Theo định lý Vi-ét ta có
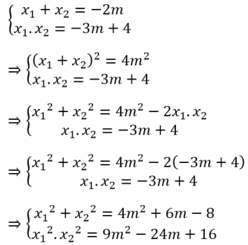
Khi đó, 
là nghiệm của phương trình
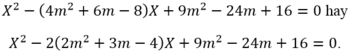
Điều kiện: \(m+2\ne0\Leftrightarrow m\ne-2\)
Ta có: \(\left(m+2\right)^2-2\left(m-1\right)x+3-m=0\)
\(\Rightarrow\Delta=4\left(m-1\right)^2-4\left(m+2\right)\left(3-m\right)\)
Để phương trình có hai nghiệm thì \(\Delta\ge0\)
\(\Rightarrow4\left(m^2-2m+1\right)-4\left(3m-m^2+6-2m\right)\ge0\)
\(\Leftrightarrow\left(m^2-2m+1\right)\ge\left(m-m^2+6\right)\)
\(\Leftrightarrow2m^2-3m-5\ge0\) \(\Leftrightarrow\left\{{}\begin{matrix}m\le-1\\m\ge\dfrac{5}{2}\end{matrix}\right.\)
Áp dụng định lí Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_1=\dfrac{2\left(m-1\right)}{m+2}\\x_1x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow\left(\dfrac{2\left(m-1\right)}{m+2}\right)^2-2\dfrac{3-m}{m+2}=\dfrac{2\left(m-1\right)}{m+2}\)
\(\Leftrightarrow\dfrac{4\left(m^2-2m+1\right)}{m^2+4m+4}=\dfrac{2m-2+6-2m}{m+2}\)
\(\Leftrightarrow\dfrac{4m^2-8m+4}{m^2+4m+4}=\dfrac{4}{m+2}\)
\(\Leftrightarrow\left(4m^2-8m+4\right)\left(m+2\right)=4m^2+16m+16\)
\(\Leftrightarrow\left(4m^3-8m^2+4m+8m^2-16m+8\right)=4m^2+16m+16\)
\(\Leftrightarrow\left(4m^3-4m^2-28m-8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m\approx3,3\\m\approx-0,3\left(loai\right)\end{matrix}\right.\)
Vậy m \(\in\left(3;4\right)\)
Câu A
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
Để PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m-1\right)^2-4\left(m+6\right)\ge0\)
\(\Leftrightarrow m^2-6m-23\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\le3-4\sqrt{2}\\m\ge3+4\sqrt{2}\end{matrix}\right.\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=1-m\\x_1x_2=m+6\end{matrix}\right.\)
\(x_1^2+x_2^2=10\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\\ \Leftrightarrow\left(1-m\right)^2-2\left(m+6\right)=10\\ \Leftrightarrow m^2-2m+1-2m-12=10\\ \Leftrightarrow m^2-4m-21=0\\ \Leftrightarrow\left[{}\begin{matrix}m=7\left(ktm\right)\\m=-3\left(tm\right)\end{matrix}\right.\Leftrightarrow m=-3\)
Phương trình có hai nghiệm
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
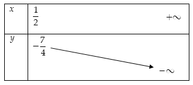
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B
Áp dụng định lí vi- et ta có: x 1 + x 2 = 3 x 1 . x 2 = 1
Ta có: x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 . x 2 = 3 2 - 2 . 1 = 7 .
Ta gọi hai nghiệm của phương trình đã cho là x 1 , x 2 . Theo hệ thức Vi-et ta có: x 1 x 2 = − 2 5 x 1 + x 2 = 9 5
⇔ M = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 − 2 x 1 x 2 = 81 25 − 2 − 2 5 = 101 25
Đáp án cần chọn là: C
\(\text{Δ}=\left(-m\right)^2-4\left(m-1\right)\)
\(=m^2-4m+4\)
\(=\left(m-2\right)^2\)>=0 với mọi m
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-m\right)}{1}=m\\x_1x_2=\dfrac{c}{a}=\dfrac{m-1}{1}=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=5\)
=>\(m^2-2\left(m-1\right)-5=0\)
=>\(m^2-2m-3=0\)
=>(m-3)(m+1)=0
=>\(\left[{}\begin{matrix}m-3=0\\m+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
\(ax^2+bx+c=0\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=\dfrac{-b}{a}\\P=x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
Ta có pt bậc 2 có 2 nghiệm là \(\dfrac{1}{x^2_1};\dfrac{1}{x^2_2}\)
\(\Rightarrow\left\{{}\begin{matrix}S'=\dfrac{1}{x^2_1}+\dfrac{1}{x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x^2_1x^2_2}\\P'=\dfrac{1}{x^2_1x^2_2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\left(\dfrac{-b}{a}\right)^2-\dfrac{2c}{a}}{\left(\dfrac{c}{a}\right)^2}\\P'=\dfrac{1}{\left(\dfrac{c}{a}\right)^2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2}{a^2}-\dfrac{2c}{a}}{\dfrac{c^2}{a^2}}\\P'=\dfrac{1}{\dfrac{c^2}{a^2}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}S'=\dfrac{\dfrac{b^2-2ca}{a^2}}{\dfrac{c^2}{a^2}}=\dfrac{b^2-2ca}{c^2}\\P'=\dfrac{a^2}{c^2}\end{matrix}\right.\)
Theo định lý Viet đảo pt bậc 2 cần lập
\(\Leftrightarrow z^2-S'z+P'=0\)
\(\Leftrightarrow z^2-\dfrac{b^2-2ca}{c^2}z+\dfrac{a^2}{c^2}=0\)