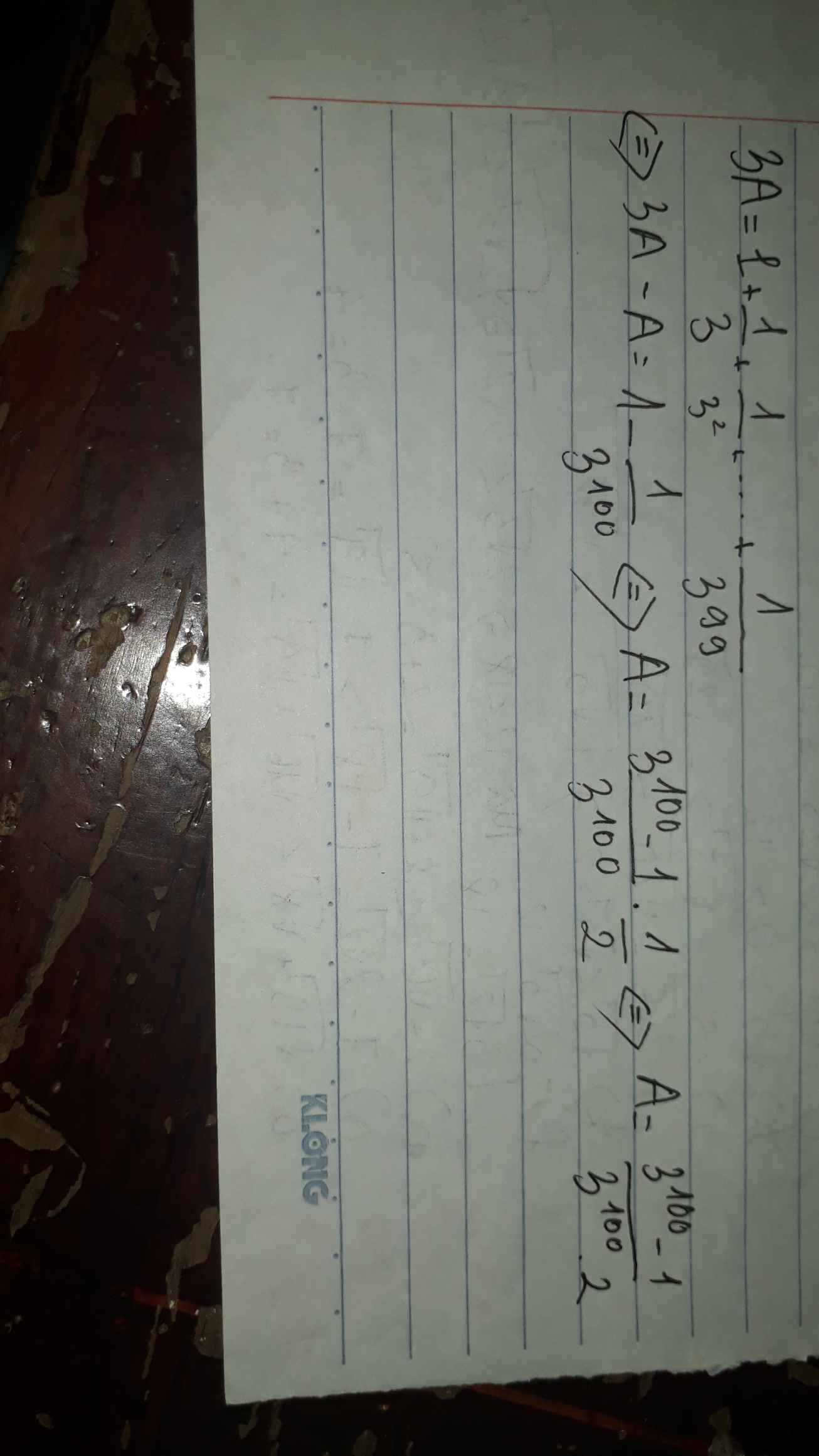Tính tổng A= 1/3 + 1/3^2 +1/3^3 + ...+1/3^100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{100}}\) ( 1 )
\(3A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\)( 2 )
Lấy ( 2 ) - ( 1 ) ta được :
\(2A=1-\frac{1}{3^{100}}\)
\(\Rightarrow A=\frac{1-\frac{1}{3^{100}}}{2}\)

\(\Rightarrow3.A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\)
\(\Rightarrow3.A-A=\left(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}\right)-\left(\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{99}}+\frac{1}{3^{100}}\right)\)
\(2.A=1-\frac{1}{3^{100}}=\frac{3^{100}-1}{3^{100}}\Rightarrow A=\frac{3^{100}-1}{2.3^{100}}\)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\\ \Leftrightarrow3A=3\left(+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\ =1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
Lấy 3A - A ta được
\(3A-A=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\right)\\
2A=1-\dfrac{1}{3^{100}}\\
\Leftrightarrow A=\dfrac{1-\dfrac{1}{3^{100}}}{2}\)


3A=1+1/3+1/3^2+...........+1/3^99
3A-A=1-1/3^100
A=(1-1/3^100):2
A = 1/3 + 1/3^2 + 1/3^3 + ... + 1/3^100
A : 3 = 1/3. ( 1/3 + 1/3^2 + ... + 1/3^100 )
A : 3 = 1/3^2 + 1/3^3 + ... + 1/3^101
A - A : 3 = 1/3 + 1/3^2 + ... + 1/3^100 - 1/3^2 - 1/3^3 - ... - 1/3^101
A . 2/3 = (1/3^2 - 1/3^2) + (1/3^3 - 1/3^3) + ... + (1/3^100 - 1/3^100) + ( 1/3 - 1/3^101 )
A . 2/3 = 0 + 0 + 0 + ... + 0 + 1/3 - 1/3^101
A . 2/3 = 1/3 - 1/3^101
=> A = 1/2 - 1/3^100.2

A = \(\dfrac{100-(1+\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{100})}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{99}{100}}\)
Xét các mẫu số của dãy phân số : \(\dfrac{1}{1};\dfrac{1}{2};....;\dfrac{1}{100}\)
ta có dãy số: 1; 2; ....;100
Dãy số trên có số số hạng là: ( 100 - 1) : 1 + 1 = 100 (số)
Tách 100 thành tổng của 100 số 1 rồi nhóm lần lượt 1 với từng phân số thuộc dãy phân số trên khi đó ta có:
A = \(\dfrac{100-(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{100})}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+.....+\dfrac{99}{100}}\)
A = \(\dfrac{(1-1)+(1-\dfrac{1}{2})+(1-\dfrac{1}{3})+....+(1-\dfrac{1}{100})}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+.....+\dfrac{99}{100}}\)
A = \(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{99}{100}}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+....+\dfrac{99}{100}}\)
A = 1