cho tam giác ABC vuông tại A có AB = 10cm, AC = 20cm. Trên cạnh AC lấy điểm D sao cho AD = 5cm. Chứng minh góc ABD = góc ACB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 10 2018
Ta có: 
Suy ra: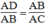 
Xét △ ADB và △ ABC, ta có:
+ Góc A chung
+ 
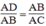(chứng minh trên)
Suy ra: △ ADB đồng dạng △ ABC (c.g.c)
Vậy ∠ (ABD) = ∠ (ACB)
15 tháng 3 2022
a: \(\widehat{ACB}=180^0-70^0-67^0=43^0\)
b: Xét ΔABD có AB=AD
nên ΔABD cân tại A
c: Xét ΔABE vuông tại E và ΔADF vuông tại F có
AB=AD
\(\widehat{BAE}\) chung
Do đó: ΔBAE=ΔDAF
d: Xét ΔABD có AF/AB=AE/AD
nên FE//BD
6 tháng 3 2023
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét ΔABD vuông tại D và ΔCAD vuông tại D có
góc DBA=góc DAC
=>ΔABD đồng dạng với ΔCAD
b: góc EAF+góc EDF=180 độ
=>AFDE nội tiếp
=>góc AFD+góc AED=180 độ
=>góc AFD=góc CED
17 tháng 6 2023
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA
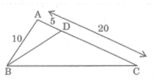
Xét tam giác ABD và tam giác ACB ta có ;
^BAD = ^BAC = 900
\(\frac{AB}{AC}=\frac{AD}{AB}=\frac{10}{20}=\frac{5}{10}=\frac{1}{2}\)
Vậy tam giác ABD ~ tam giác ACB ( c.g.c )
=> ^ABD = ^ACB ( 2 góc tương ứng )