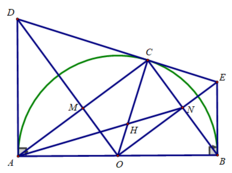
Cho (O) đường kính AB, vẽ tiếp Ax, By. Lấy C thuộc (O), tiếp tuyến tại C cắt Ax, By lần lượt tại D, E
a) chứng minh AD + BE= DE và góc DOE = \(90^o\)
b) Chứng minh AB là tiếp tuyến của đường tròn đường kính DE
c) AE cắt BD tại I. Chứng minh CI vuông góc AB


b) Gọi M là trung điểm DE.
\(\Delta ODE\)vuông tại O (vì \(\widehat{DOE}=90^0\)), có M là trung điểm DE
\(\Rightarrow\)M là tâm đướng tròn ngoại tiếp \(\Delta ODE\)(với đường kình DE)
\(\Rightarrow\)O thuộc đường tròn đường kình DE hay \(O\in\left(M\right)\)
Dễ thấy AD//BE \(\left(\perp AB\right)\)\(\Rightarrow\)Tứ giác ABED là hình thang
Xét hình thang ABED (AD//BE) có O, M lần lượt là trung điểm của AB, DE
\(\Rightarrow\)OM là đường trung bình của hình thang ABED
\(\Rightarrow\)OM//AD, mà \(AD\perp AB\)(DA là tiếp tuyến tại A của (O))
\(\Rightarrow AB\perp OM\)tại O
Mà \(O\in\left(M\right)\left(cmt\right)\)\(\Rightarrow\)AB là tiếp tuyến của (M) hay đường tròn đường kính DE (đpcm)
Mình không vẽ hình vì sợ duyệt, không hiện lên được. Mình cũng sẽ chia bài này thành 3 câu trả lời cho 3 câu a,b,c cho ngắn. Để dài quá nó cũng bảo duyệt.
a) Xét đường tròn (O) có 2 tiếp tuyến tại A và C cắt nhau tại D (gt) \(\Rightarrow AD=CD\)(tính chất 2 tiếp tuyến cắt nhau) (1)
Tương tự, ta có \(BE=CE\)(2)
Vì \(C\in DE\left(gt\right)\)\(\Rightarrow CD+CE=DE\)(3)
Từ (1), (2) và (3) \(\Rightarrow AD+BE=DE\)(đpcm thứ nhất)
Đồng thời, theo tính chất của 2 tiếp tuyến cắt nhau, ta có OD, OE lần lượt là tia phân giác của \(\widehat{AOC},\widehat{BOC}\)
\(\Rightarrow\hept{\begin{cases}\widehat{DOC}=\frac{\widehat{AOC}}{2}\\\widehat{EOC}=\frac{\widehat{BOC}}{2}\end{cases}}\)\(\Rightarrow\widehat{DOE}=\widehat{DOC}+\widehat{EOC}=\frac{\widehat{AOC}+\widehat{BOC}}{2}=\frac{180^0}{2}=90^0\)(đpcm thứ hai)