Cho tam giác ABC. Gọi E là trung điểm của AB. Trên tia đối của tia EC lấy điểm M sao cho: EM = EC.
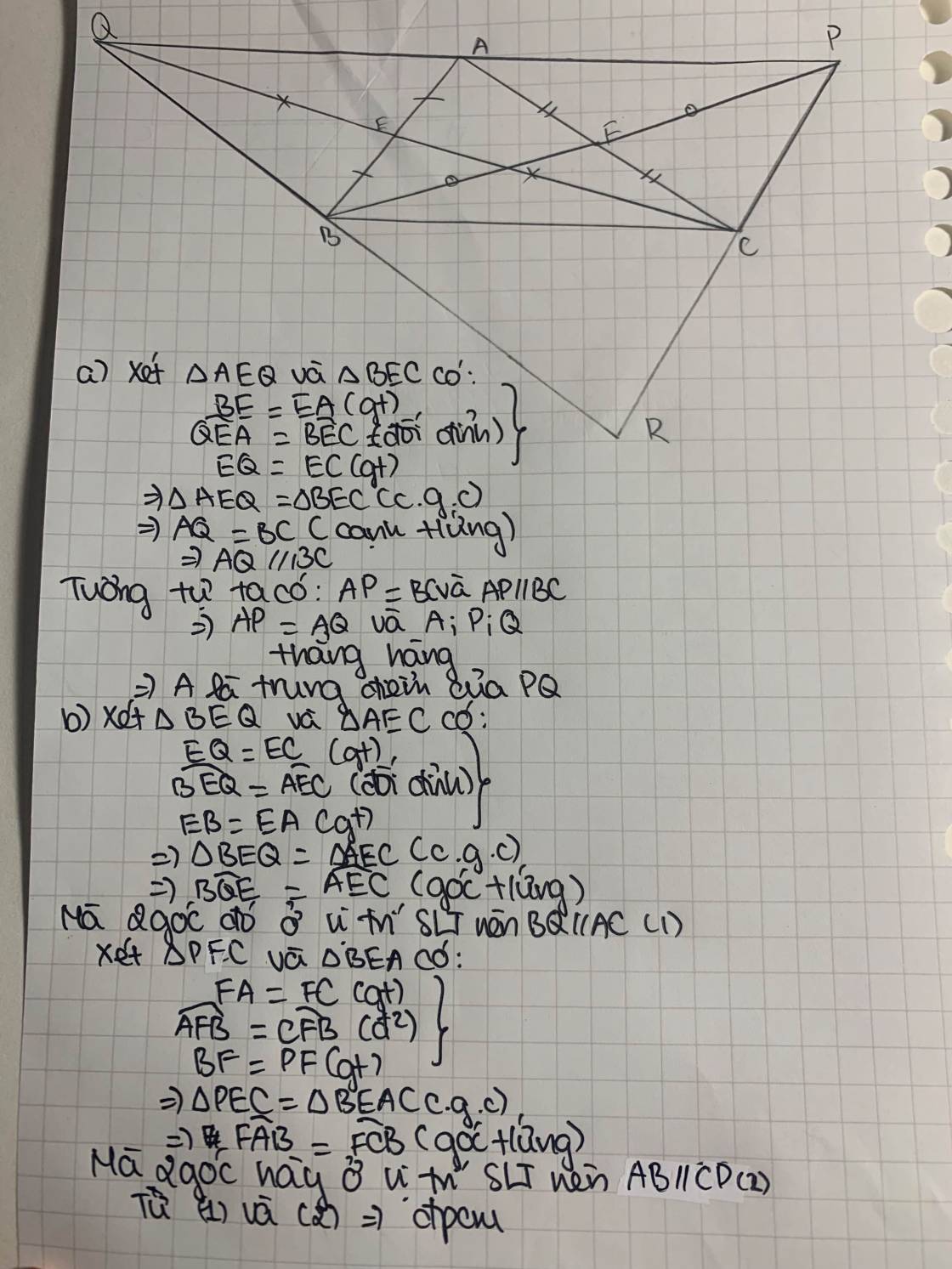
a. Chứng minh: \(\Delta AEM=\Delta BEC\)
b. Chứng minh AM//BC
c. Gọi F là trung điểm của AC. Trên tia đối của tia FB lấy điểm N sao cho: FN = FB. Chứng minh A là trung điểm của MN

 Nhãn
Nhãn