giải lẹ giúp mình....
cho tam giác DEG cân tại D. Kẻ ER vuông góc DG ( R thuộc DG)
CHứng minh : DE^2 + DG^2 + DG^2 = 2DR^2 + 3ER^2 + GR^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
a: Xét ΔDEG có
H là trung điểm của EG
HK//DG
Do đó: K là trung điểm của DE
Xét ΔDEG có
H là trung điểm của EG
K là trung điểm của DE
Do đó: HK là đường trung bình của ΔDEG
19 tháng 12 2016
Để CM \(HM^2=HB.HC\):
Trên đường thẳng qua \(C\) vuông góc \(BC\) ta chọn điểm \(T\) sao cho \(TM\) là phân giác \(BTC\).
Do có hệ thức \(\frac{MB}{MC}=\frac{DB}{DC}\) suy ra luôn \(TN\) là phân giác ngoài của \(BTC\).
Vậy tam giác \(MTN\) là vuông nên \(HT=HN\), hay \(\widehat{HTN}=\widehat{HNT}=\widehat{MTC}=\widehat{MTB}\).
Suy ra \(\widehat{BTH}\) vuông và ta có \(HB.HC=HT^2=HN^2\).
P/S: Nếu cho 4 điểm \(A,B,C,D\) thẳng hàng theo thứ tự đó và thoả \(\frac{BA}{BC}=\frac{DA}{DC}\) thì 4 điểm này gọi là hàng điều hoà (giống chân đường phân giác trong và ngoài ấy).
Khi đó, nếu gọi \(T\) là trung điểm \(BD\) thì ta có hệ thức: \(TB^2=TA.TC\) và \(CD.CB=CA.CT\).
18 tháng 12 2016
(Sao mấy bài hình học của bạn thấy nhiều "hàng điều hoà" thế?)
Gọi \(H\) là trung điểm \(MN\). CM được \(HC.HB=HM^2=HD^2\).
Tức là tam giác \(HCD\) và \(HDB\) đồng dạng, cho ta 2 góc sau bằng nhau: \(HDC=HBD=\alpha\).
Do \(ACB=2\alpha\) nên \(CHD=\alpha=CBD\).
Vậy tam giác \(BDH\) cân tại \(D\) và ta suy ra đpcm.
NH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 7 2023
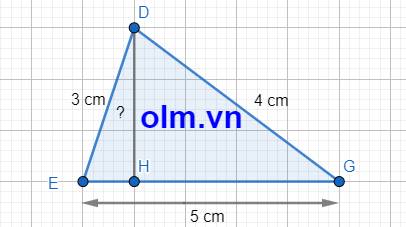
Gọi độ dài cạnh EH là \(x\) (cm); 0 < \(x< 5\)
Độ dài cạnh HG là: 5 - \(x\) (cm)
Xét tam giác vuông HDE vuông tại H, theo pytago ta có:
DH2 = 32 - \(x^2\) = 9 - \(x^2\)(1)
Xét tam giác vuông DHG vuông tại H theo pytago ta có:
DH2 = 42 - (5 - \(x\))2 = -\(x^2\) + 10\(x\) - 9(2)
Từ (1) và (2) ta có:
-\(x^2\) + 10\(x\) - 9 = 9 - \(x^2\)
10\(x\) = 18
\(x\) = 1,8 (thỏa mãn)
Thay \(x\) = 1,8 vào biểu thức (1) ta có:
DH2 = 9 - (1,8)2 = 5,76
DH = \(\sqrt{5,76}\) = 2,4 (cm)
Kết luận: độ dài đoạn DH là 2,4 cm