Cho Tam giác ÁC vuông góc tại A từ trung điểm K của BC kẻ đường vuông góc với AK cắt AB và AC tại D và E gọi I là trung điểm của DE chứng minh rằng AI vuông góc với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
6 tháng 3 2018
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Lê Xuân Huy - Toán lớp 7 - Học toán với OnlineMath
CH
Cô Hoàng Huyền
Admin
VIP
6 tháng 3 2018
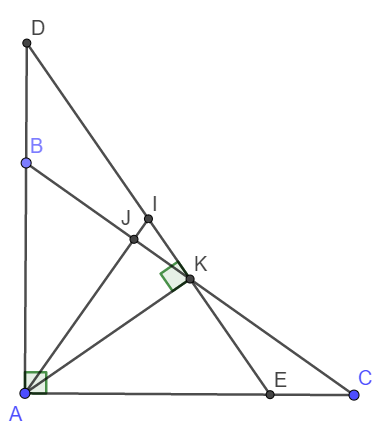
a) Xét tam giác vuông ABC có K là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: KB = KA
Hay tam giác KAB cân tại K, suy ra \(\widehat{KBA}=\widehat{KAB}\)
Xét tam giác vuông ADE có I là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: ID = IA
Hay tam giác IDA cân tại I, suy ra \(\widehat{IAB}=\widehat{IDA}\)
Vậy nên ta có: \(\widehat{KBA}+\widehat{IAB}=\widehat{KAB}+\widehat{IDA}=90^o\left(\widehat{DKA}=90^o\right)\)
Gọi giao điểm của BC và AI là J.
Xét tam giác ABJ có \(\widehat{JBA}+\widehat{JAB}=90^o\Rightarrow\widehat{BJA}=90^o\)
Vậy nên \(AI\perp BC.\)
b) Ta thấy ngay \(DE=2AI;BC=2AK\)
Mà theo quan hệ giữa đường vuông góc và đường xiên thì \(AI\ge AK\)
Vậy nên \(DE\ge BC\).