Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trả lời :
1. Tìm tỉ số phần trăm của 2 số
Để tìm tỉ số phần trăm của số A so với số B ta chia số A cho số B rồi nhân với 100.
Ví dụ 1. Một lớp học có 28 em, trong đó có 7 em học giỏi toán. Hãy tìm tỉ số phần trăm học sinh giỏi toán so với sĩ số của lớp?
Phân tích: Ta phải tìm tỉ số phần trăm của 7 em so với 28 em. Như vậy nếu sĩ số của lớp là 100 phần thì 7 em sẽ là bao nhiêu phần?
Giải: Tỉ số phần trăm học sinh giỏi toán so với học sinh cả lớp là:
7 : 28 = 0,25
0,25 = 25%
Đáp số : 25%
2. Tìm số phần trăm của một số
Thí dụ 1. Chiếc xe đã đi được 40% chiều dài của con đường dài 250 km. Tính phần còn lại của con đường mà xe còn phải đi?
Phân tích: Muốn tìm 40% của 250 tức là 250 có 100 phần thì 40 phần sẽ là bao nhiêu?
Giải: Xe đó đã đi được:
40% x 250 = 100 (km).
Do đó phần đường còn lại phải đi là:
250 - 100 = 150 (km).
Đáp số: 150 km.
Trong toán học, phần trăm là tỉ số thể hiện dưới dạng phân số có mẫu số là 100. Ký hiệu thường dùng là ký hiệu phần trăm "%". Ví dụ, 20% (đọc là "hai mươi phần trăm") tương đương với 20/100, nói cách khác là 0,2. ... Phần trăm thường được dùng để biểu thị độ lớn tương đối của một lượng so với một lượng khác.
Nếu bạn nhân thì nhân với số % xong chia cho 100
Nếu bạn chia thì nhân 100 rồi chi số %

Tam giác đều cũng tương tự như tam giác thường. Tức là đều có cách tính diện tích là tích của chiều cao và cạnh đáy sau đó chia 2. Như vậy, với bài toán cho biết hai dữ liệu là chiều cao và chiều dài cạnh đáy thì chúng ta áp dụng công thức S = (a x h) / 2.
HT

Bạn xem hướng dẫn rồi vận dụng để làm nhé.
Để đổi từ phân số sang tỉ số phần trăm thì ta chuyển phân số đã cho thành số thập phân rồi nhân với 100%.
Ví dụ : 1/5 = 0,2 = 0,2 x 100% = 20%

PTHH: \(A+B+...\xrightarrow[]{\text{điều kiện phản ứng}}C+D+...\)
\(m_{dd\text{ sau phản ứng}}=m_{\text{tổng khối lượng của các chất tham gia phản ứng kể cả dd}}-m_{\text{chất kết tủa}}-m_{\text{chất khí}}\)
Khi đó \(C\%_{muối\left(\text{tan trong nước}\right)}=\dfrac{m_{muối\left(\text{tan trong nước}\right)}}{m_{dd\text{ sau phản ứng}}}.100\%\)
tính khối lượng dd
tính khối lượng ct
cuối cùng tính C%
\(C\%=\dfrac{m_{ct}}{m_{\text{dd}}}.100\%\)

công thức :
6.tổng hai lập phương :
A3 + B3 = ( A+B).(A2 - AB + B2 )
7. hiệu hai lập phương :
A3 - B3 = ( A-B).( A2+ AB + B2 )
*Sxl
công thức 6.Tổng 2 lập phương
với a và b là biểu thức tùy ý ta có:A3+B3 =(A+B)(A2-AB+B2)
công thức 7:hiệu 2 lập phuong
A3-B3=(A-B)(A2+AB+B2)

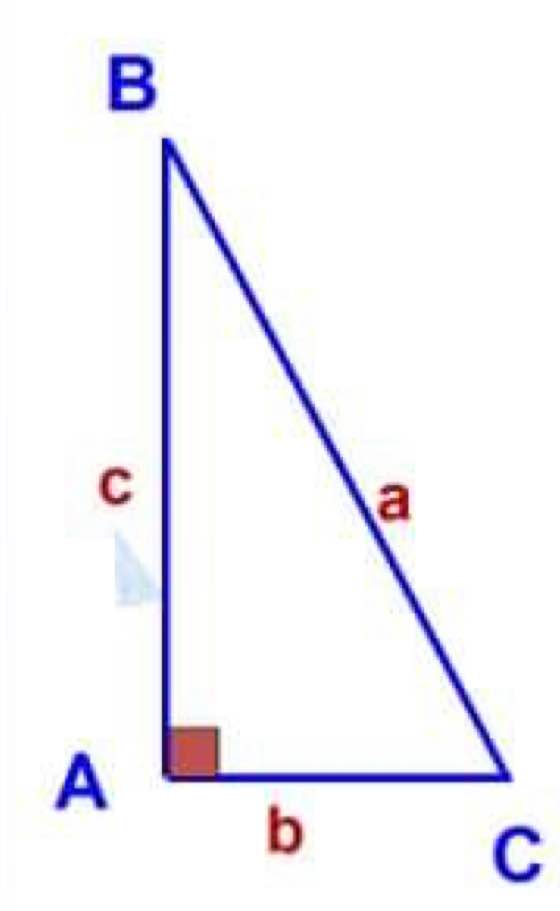
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)

MX = 17.2 = 34 (g/mol)
\(m_S=\dfrac{94,12.34}{100}=32\left(g\right)=>n_S=\dfrac{32}{32}=1\left(mol\right)\)
\(m_H=\dfrac{5,88.34}{100}=2\left(g\right)=>n_H=\dfrac{2}{1}=2\left(mol\right)\)
=> CTHH: H2S
Khi so sánh 2 số nào đó người ta có thể dùng khái niệm tỉ số phần trăm để nói số này bằng bao nhiêu phần trăm số kia. Chẳng hạn 20 bằng 20% của 100, năng suất lao động của công nhân A bằng 70% năng suất lao động của công nhân B, học sinh giỏi của lớp chiếm 75% sĩ số lớp, có 10% học sinh của trường được tuyên dương,...
lấy số tổng coi là 100% , lấy số tổng chia 100 là coi 100 này là 100 % lấy tổng chia 100 là ra 1 %