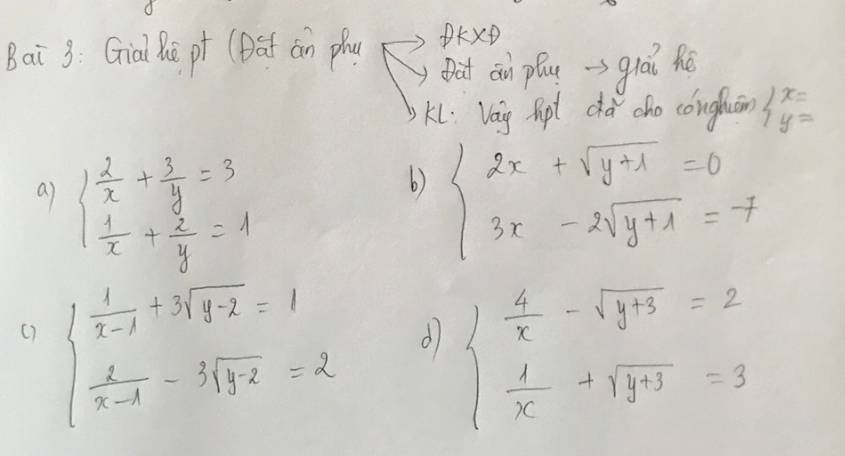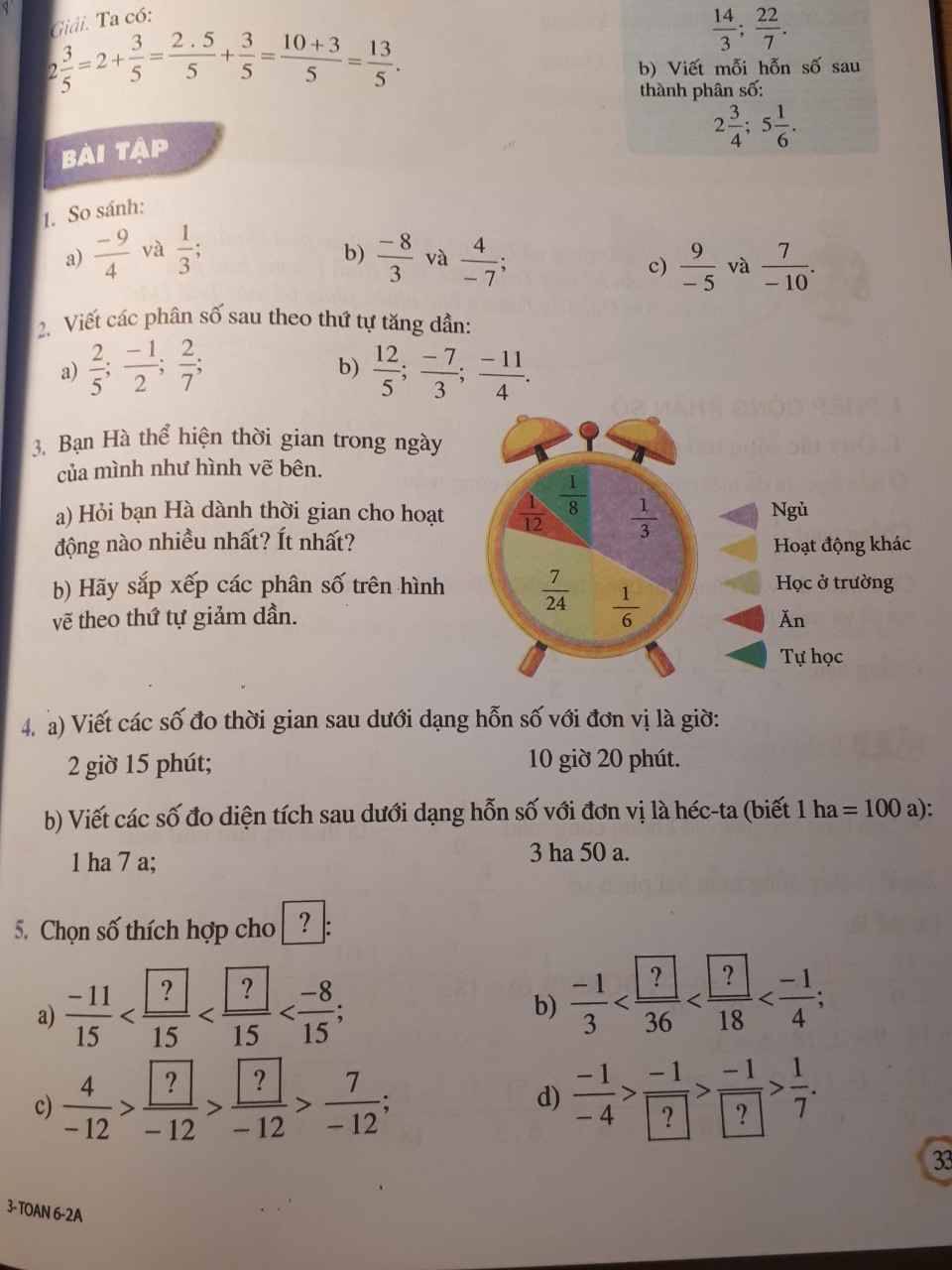Giúp mình câu d,cảm ơn trước...
Đọc tiếp
Giúp mình câu d,cảm ơn trước ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KA
1
TP
2 tháng 8 2021
d) Gọi x,y lần lượt là số mol Al, Fe
\(\left\{{}\begin{matrix}27x+56y=8,3\\1,5x+y=0,25\end{matrix}\right.\)
=> x=0,1 ; y=0,1
Kết tủa : Al(OH)3, Fe(OH)2
Bảo toàn nguyên tố Al: \(n_{Al\left(OH\right)_3}=n_{Al}=0,1\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{Fe\left(OH\right)_2}=n_{Fe}=0,1\left(mol\right)\)
=> \(m=0,1.78+0,1.90=16,8\left(g\right)\)
Nung kết tủa thu được chất rắn : Al2O3 và FeO
Bảo toàn nguyên tố Al: \(n_{Al_2O_3}.2=n_{Al}\Rightarrow n_{Al_2O_3}=0,05\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{FeO}=n_{Fe}=0,1\left(mol\right)\)
=> \(a=0,05.102+0,1.72=12,3\left(g\right)\)
NT
2
NM
30 tháng 10 2023
\(d,-\dfrac{3}{26}.\left(-\dfrac{15}{19}\right)+\dfrac{2}{19}.\left(-\dfrac{3}{26}\right)\\=-\dfrac{3}{26}.\left(-\dfrac{15}{19}+\dfrac{2}{19}\right)\\ =-\dfrac{13}{19}.\left(-\dfrac{3}{26}\right)\\ =\dfrac{3}{38}. \)
VN
Võ Ngọc Phương
VIP
30 tháng 10 2023
d) \(\dfrac{-3}{26}\times\left(\dfrac{-15}{19}\right)+\dfrac{2}{19}\times\dfrac{-3}{26}\)
\(=\dfrac{-3}{26}\times\left[\left(\dfrac{-15}{19}\right)+\dfrac{2}{19}\right]\)
\(=\dfrac{-3}{26}\times\dfrac{-13}{19}\)
\(=\dfrac{3}{38}\)
AH
1
16 tháng 9 2023
b: ĐKXĐ: y>=-1
Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
2a+b=0 và 3a-2b=-7
=>4a+2b=0 và 3a-2b=-7
=>a=-1 và b=2
=>x=-1 và y+1=4
=>x=-1 và y=3
c: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
a+3b=1 và 2a-3b=2
=>3a=3 và a+3b=1
=>a=1 và b=0
=>x-1=1 và y-2=0
=>x=2 và y=2
d: ĐKXĐ: x<>0 và y>=-3
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
4a-b=2 và a+b=3
=>5a=5 và a+b=3
=>a=1 và b=2
=>x=1 và y+3=4
=>x=1 và y=1
VT
1
22 tháng 10 2021
Bài 6:
a: \(M=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
VT
1
22 tháng 10 2021
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
NY
1
17 tháng 3 2022
a, Gọi chiều rộng ban đầu là x(m) x>0
Chiều dài ban đầu : x+10(m)
Chiều rộng sau khi được tăng: x+5(m)
Chiều dài sau khi giảm: x+10-2=x+8(m)
Theo bài ra ta có pt
(x+8)(x+5)-x(x+10)=100
Giải ra được x=20(m)
Chiều dài : 20=10=30(m)
Diện tích mảnh vườn:20.30=600(m\(^2\))
b, Gọi vận tốc trung bình của xe mày là x(km/h) x>0
Vận tốc tb của ô tô là : x+6(km/h)
Theo bài ra ta có pt
2x+2(x+6)=140
Giải ra được x=32(km/h)
Vtb của ô tô là 32+6=38(km/h)
HL
5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 1
Câu 1:
a; \(\dfrac{-9}{4}\) < 0; \(\dfrac{1}{3}\) > o
\(\dfrac{-9}{4}\) < \(\dfrac{1}{3}\)
b; \(\dfrac{-8}{3}\) < - 1
\(\dfrac{4}{-7}\) > - 1
Vậy \(\dfrac{-8}{3}\) < \(\dfrac{4}{-7}\)
c; \(\dfrac{9}{-5}\) < - 1
\(\dfrac{7}{-10}\) > - 1
Vậy \(\dfrac{9}{-5}\) < \(\dfrac{7}{-10}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
4 tháng 1
Câu 2:
a; Viết các phân số theo thứ tự tăng dần
\(\dfrac{-1}{2}\); \(\dfrac{2}{7}\); \(\dfrac{2}{5}\)
b; \(\dfrac{-11}{4}\); \(\dfrac{-7}{3}\); \(\dfrac{12}{5}\)
TQ
5
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
17 tháng 7 2021
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)