Cho tam giác ABC có 3gócA=4góB=6gócC. Kẻ AM vuông góc với BC tại M. So sánh AM, BM,...
Đọc tiếp
- Cho tam giác ABC có 3gócA=4góB=6gócC. Kẻ AM vuông góc với BC tại M. So sánh AM, BM, CM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
S
0
Những câu hỏi liên quan
KV
11 tháng 3 2023
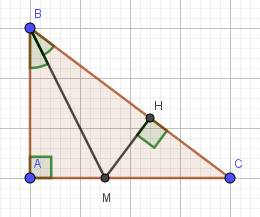
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
3 tháng 4 2017
a) Tam giác ABC vuông tại A có \(BC^2=AB^2+AC^2\)
=>BC2=32+42=25
=>BC=5
Vậy BC=5 cm
b) Xét tam giác BHM vuông tại H và tam giác CKM vuông tại K có
MC=MB( vì M là trung điểm của BC)
CMK=BHM( 2 góc đối đỉnh)
=> tam giác BHM= tam giác CKM ( cạnh huyền- góc nhọn)
c) Xét tam giác HMI vuông tại I có HM>HI ( cạnh huyền lớn nhất) (1)
Có tam giác BHM= tam giác CKM ( câu b)
=>HM=MK (2)
Từ (1) và (2) =>MK>HI
d) Có \(\Delta BHM=\Delta CKM\)( theo câu b)
=> BH=KC
Xét tam giác BKC có KC+BK>BC ( bất đẳng thức tam giác) (3)
Thay BH=KC vào (3) ta có BH+BK>BC
11 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
b: Xét ΔABM vuông tại A và ΔKBM vuông tại K có
BM chung
góc ABM=góc KBM
=>ΔBAM=ΔBKM
c: AM=MK
MK<MC
=>AM<MC
d: Xét ΔMAD vuông tại A và ΔMKC vuông tại K có
MA=MK
góc AMD=góc KMC
=>ΔMAD=ΔMKC
=>AD=KC
Xét ΔBDC có BA/AD=BK/KC
nên AK//DC