Biết \(7x=3y\) và \(x-y=16\).Vậy \(x.y\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
28 tháng 2 2016
7x = 3y => x/3 = y/7
Áp dụng tính chất của dãy tỉ số = nhau ta có:
x/3 = y/7 = x-y / 3-7 = 16/-4 = -4
+) x/3 = -4 => x = -4 . 3 = -12
+) y/7 = -4 => y = -4 . 7 = -28
=> xy = 9-12).(-28) = 336
TN
5
CU
17 tháng 7 2019
\(\frac{x}{5}=\frac{y}{7}=k\Rightarrow\hept{\begin{cases}x=5k\\y=7k\end{cases}}\)
\(x\cdot y=140\)
\(\Rightarrow5k\cdot7k=140\)
\(\Rightarrow35k^2=140\)
\(\Rightarrow k^2=4\)
\(\Rightarrow k=\pm2\)
\(k=2\Rightarrow\hept{\begin{cases}x=2\cdot5=10\\y=2\cdot7=14\end{cases}}\)
\(k=-2\Rightarrow\hept{\begin{cases}x=-2\cdot5=-10\\y=-2\cdot7=-14\end{cases}}\)
\(7x=3y\)
\(\Rightarrow\frac{x}{3}=\frac{y}{7}=k\Rightarrow\hept{\begin{cases}x=3k\\y=7k\end{cases}}\)
\(\Rightarrow x\cdot y=3k\cdot7k=2100\)
\(\Rightarrow21k^2=2100\)
\(\Rightarrow k^2=100\)
\(\Rightarrow k=\pm10\)
\(k=10\Rightarrow\hept{\begin{cases}x=10\cdot3=30\\y=10\cdot7=70\end{cases}}\)
\(k=-10\Rightarrow\hept{\begin{cases}x=-10\cdot3=-30\\y=-10\cdot7=-70\end{cases}}\)
SB
4
KD
17 tháng 8 2018
\(7x=3y\)
\(\Rightarrow\frac{x}{3}=\frac{y}{7}\)
Áp dụng tính chất của tỉ số bằng nhau, ta có :
\(\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}=\frac{16}{-4}=-4\)
Suy ra :
\(\frac{x}{3}=-4\Leftrightarrow x=-12\)
\(\frac{y}{7}=-4\Leftrightarrow y=-28\)
Vậy :.......
13 tháng 10 2016
a) Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow x=2k\)
\(\Rightarrow y=5k\)
\(\Rightarrow xy=2k.5k=10k^2\)
\(\Rightarrow10k^2=10\)
\(\Rightarrow k^2=\frac{10}{10}=1\Rightarrow\left[\begin{array}{nghiempt}k=1\\k=-1\end{array}\right.\)
Với \(k=1\)
\(\Rightarrow x=2k=2.1=2\)
\(\Rightarrow y=5k\Rightarrow y=5.1=5\)
Với \(k=-1\)
\(\Rightarrow x=2k=-1.2=-2\)
\(\Rightarrow y=5k=-1.5=-5\)
13 tháng 10 2016
b) \(7x=3y\Rightarrow\frac{7x}{21}=\frac{3y}{21}\Rightarrow\frac{x}{7}=\frac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{7}=\frac{y}{3}=\frac{x-y}{7-3}=\frac{16}{4}=4\)
- \(x=4.7=28\)
- \(y=4.3=12\)
Vậy: \(x=28,y=12\)
VV
1
4 tháng 10 2016
a) \(7x=3y\Rightarrow\)\(\frac{x}{3}=\frac{y}{7}\)
Đặt \(\frac{x}{3}=\frac{y}{7}=k\Rightarrow x=3k;y=7k\)
Có: x.y=84
\(\Rightarrow3k\cdot7k=84\)
\(\Rightarrow k^2=4\Rightarrow\left[\begin{array}{nghiempt}k=2\\k=-2\end{array}\right.\)
Với k=2 thì x=6 ;y=14
Với k=-2 thì x=-6 ;y =-14
b) \(7x=3y\Rightarrow\)\(\frac{x}{3}=\frac{y}{7}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{7}=\frac{5y-2x}{5\cdot7-2\cdot3}=\frac{-4}{29}\)
=> \(\begin{cases}x=-\frac{12}{29}\\y=-\frac{28}{29}\end{cases}\)
c) \(2x=3y=5z\)
\(\Leftrightarrow\)\(\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\)
=> \(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)
Áp dụng tc của dãy tỉ số bằng nhau ta co:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+2y-3z}{15+2\cdot10-3\cdot6}\)
thiếu đề
4 tháng 10 2016
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+2y-3z}{15+2\cdot10-3\cdot6}=\frac{10}{17}\)
=>\(\begin{cases}x=\frac{150}{17}\\y=\frac{100}{17}\\z=\frac{60}{17}\end{cases}\)
@VỘI VÀNG QUÁ
N
5 tháng 11 2021
Áp dụng TCDTSBN:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{16}{4}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=28\\y=12\end{matrix}\right.\)
5 tháng 11 2021
Nhầm ròi iem ơi :>>
\(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
CM
30 tháng 3 2017
Từ giả thiết 7x = 3y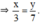 
Theo tính chất của dãy tỉ số bằng nhau ta có: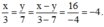 
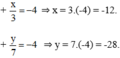
Vậy x = -12 và y = -28.
LD
9 tháng 7 2016
7x=3y => x/3=y/7=(x-y)/-4 = 16: -4 = -4
=>x= -4.3=-12
=>y= -4.7= -28
HT
9 tháng 7 2016
7x = 3y
=> \(\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}=\frac{16}{-4}=-4\)(Tính chất dãy tỉ số bằng nhau)
=> x = -4 . 3 = -12
y = -4 . 7 = -28
NH
12
NX
1 tháng 9 2016
Ta có : 7x = 3y
\(\Rightarrow\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}=\frac{16}{-4}=-4\)
\(\Rightarrow\frac{x}{3}=-4\Rightarrow x=-4\cdot3=-12\)
\(\Rightarrow\frac{y}{7}=-4\Rightarrow y=-4\cdot7=-28\)
DS
1 tháng 9 2016
7x=3y
=>x=3/7y
x-y=16
=>3/7y-y=16
-4/7y=16
y=16.-7/4
y=-28.
x tự tìm nha bạn.
ta có:7x=3y=x/3=y/7 và x-y=16
Áp dụng tính chất của dãy tỉ số bằng nhau
=>x/3=y=7=x-y/3-7=16/-4=-4
=>x/3=4=4*3=12
=>y/7=4=7*4=28
Vậy x.y=12*28=336
\(7x=3y=>\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}\)= \(\frac{16}{-4}=-4\)
=> \(\frac{x}{3}=-4=>x=-12\)
\(\frac{y}{7}=-4=>y=-28\)
Vậy ......
K NHA