Câu 25:Với giá trị nào của m thì phương trình: mx^2+2(m-2)x+m-3=0 có 2 nghiệm phân biệt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình có 2 nghiệm pb khi:
\(\Delta=m^2+4m^2>0\Leftrightarrow5m^2>0\)
\(\Rightarrow m\ne0\)

x 2 – 2(m+3)x + m 2 +3=0 (1)
Ta có: ∆ ' = - m + 3 2 -1.( m 2 +3) = m 2 + 6m + 9 – m 2 - 3
= 6m +6
Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi:
∆ ' > 0 ⇔ 6m + 6 > 0 ⇔ 6m > -6 ⇔ m > -1
Vậy m > -1 thì phương trình đã cho có 2 nghiệm phân biệt

Phương trình mx2 – 2(m – 1)x + m – 3 = 0
có a = m; b’ = − (m – 1); c = m – 3
Suy ra = [− (m – 1)]2 – m(m − 3) = m + 1
Để phương trình có hai nghiệm phân biệt thì
a ≠ 0 Δ ' > 0 ⇔ m ≠ 0 m + 1 > 0 ⇔ m ≠ 0 m > − 1
Nên với đáp án A: m = − 5 4 < − 1
thì phương trình không có hai nghiệm phân biệt
Đáp án cần chọn là: A

x 2 + 2(m + 5)x + 6m - 30 = 0
a) Δ' = b ' 2 - ac = m + 5 2 - (6m - 30)
= m 2 + 10m + 25 - 6m + 30 = m 2 + 4m + 55
= m 2 + 4m + 4 + 51 = m + 2 2 + 51 > 0 ∀m
Vậy phương trình đã cho luôn có 2 nghiệm phân biệt với mọi m

Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 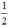
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 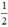
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 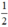
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 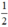 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 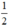 và vô nghiệm khi m >
và vô nghiệm khi m > 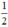

\(\text{Δ}=\left(-m\right)^2-4\left(-2m^2+3m-2\right)\)
\(=m^2+8m^2-12m+8\)
\(=9m^2-12m+8\)
\(=9m^2-12m+4+4=\left(3m-2\right)^2+4>0\)
Do đó: PHương trình luôn có hai nghiệm phân biệt
Giá trị nào của m thì phương trình (m -3)x^2 +(m +3)x -(m +1) = 0 (1) có hai nghiệm dương phân biệt?

TH1: m=3
Pt sẽ là (3+3)x-(3+1)=0
=>6x-4=0
=>x=2/3
=>Loại
TH2: m<>3
Δ=(m+3)^2-4(m-3)(-m-1)
=m^2+6m+9+4(m-3)(m+1)
=m^2+6m+9+4(m^2-2m-3)
=5m^2-2m-3
Để phương trình có hai nghiệm dương phân biệt thì
5m^2-2m-3>0 và (-m-3)/(m-3)>0 và (-m-1)/(m-3)>0
=>(m-1)(5m+3)>0 và (m+3)/(m-3)<0 và (m+1)/(m-3)<0
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< -\dfrac{3}{5}\end{matrix}\right.\\-3< m< 3\\-1< m< 3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-1< m< -\dfrac{3}{5}\\1< m< 3\end{matrix}\right.\)
Câu 25: \(ĐK:m\ne0\)
PT có 2 nghiệm pb
\(\Leftrightarrow\Delta=4\left(m-2\right)^2-4m\left(m-3\right)>0\\ \Leftrightarrow4m^2-16m+16-4m^2+12m>0\\ \Leftrightarrow16-4m>0\Leftrightarrow m< 4\)
Vậy \(m< 4;m\ne0\)