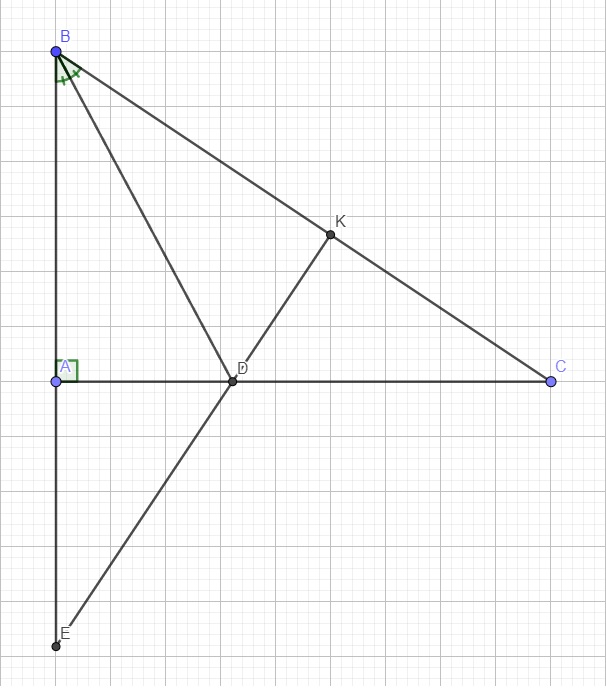
Cho tam giác ABC vuông tại B và BA BC. Trên cạnh BC, lấy điểm D BD BC , trên tia đối của tia BA lấy điểm E sao cho BD BE.a Chứng minh hai tam giác CBE và tam giác BDA bằng nhau, từ đó suy ra góc CEB góc BDAb Kéo dài AD, cắt CE tại H.Chứng minh tam giác AEH vuông tại H
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2023
A: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=90 độ
b: BA=BE
DA=DE
=>BD là trung trực của AE
DA=DE
DE<DC
=>DA<DC
12 tháng 5 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
=>AD=ED
b: BA=BE
DA=DE
=>BD là trung trực của AE
AD=DE
DE<DC
=>AD<DC
c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>E,D,F thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
a.
Xét \(\Delta BAD\) và \(\Delta BKD\) có:
\(\left\{{}\begin{matrix}BA=BK\left(gt\right)\\\widehat{ABD}=\widehat{KBD}\left(gt\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BAD=\Delta BKD\left(c.g.c\right)\)
\(\Rightarrow AD=DK\)
b.
Cũng do \(\Delta BAD=\Delta BKD\Rightarrow\widehat{BKD}=\widehat{BAD}\)
Mà \(\widehat{BAD}=90^0\left(gt\right)\Rightarrow\widehat{BKD}=90^0\)
\(\Rightarrow DK\perp BC\)
\(\Rightarrow\widehat{ABK}=\widehat{CDK}\) (cùng phụ \(\widehat{ACB}\))
c.
Xét hai tam giác ADE và KDC có:
\(\left\{{}\begin{matrix}AD=DK\left(cmt\right)\\\widehat{ADE}=\widehat{KDC}\left(\text{đối đỉnh}\right)\\DE=DC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ADE=\Delta KDC\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAE}=\widehat{DKC}=90^0\)
\(\Rightarrow\widehat{BAE}=\widehat{BAC}+\widehat{DAE}=90^0+90^0=180^0\)
\(\Rightarrow B,A,E\) thẳng hàng
12 tháng 5 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE
b: Xet ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
c: BA=BE
DA=DE
=>BD là trung trực của AE
AD=DE
DE<DC
=>AD<DC
9 tháng 12 2018
a) Xét tam giác ABM và tam giác DCM có:
AM = DM (gt)
BM = MC (gt)
góc BMA = góc DMC (2 góc đối đỉnh)
=> tam giác ABM = tam giác DCM (c.g.c)
b) Vì tam giác ABM = tam giác DCM (cmt)
=> góc ABM = góc DCM (2 góc tương ứng)
mà 2 góc này so le trong
=> AB//DC
c) Xét tam giác ABM và tam giác ACM có:
AB = AC (gt)
BM = MC (gt
AM là cạnh chung
=> tam giác ABM bằng tam giác ACM (c.c.c)
=> góc BMA bằng góc AMC
=> góc BMA = góc AMC = 1/2(góc BMA + góc AMC)
mà góc BMA + góc AMC = 180o (2 góc kề bù)
=> góc BMA = góc AMC = 1/2.180o = 90o
=> AM vuông góc với BC