Thầy cô và các bạn giúp e bài này ạ . 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không phải khi gv onl mới tick cho các bạn đâu ._. Những bạn trả lời đúng và chính xác mà gv không onl thì sẽ được chọn sau. Bạn có thể gửi câu đó cho gv xem nếu bạn chắc chắn nó hay và đúng....Lúc nào cũng khiếu nại như vầy thì gv trang nào mà chịu cho nổi ? ![]()

Nguyễn Linh nói đúng đấy em trả lời nhiều rồi mà không được tick .![]()
Mong các thầy cô hoc24 xem xét kĩ hơn , khắc phục việc này .![]()
Em xin cảm ơn . 
![]()

Bạn à, không phải vì online mà Giáo viên của Hoc24h mới tick cho bạn đâu. Mình nghĩ chắc trong câu trả lời của bạn còn mắc về nỗi diễn đạt, cũng như cách làm chưa được tối ưu, ngôn ngữ chưa chính xác,trình bày chưa được đẹp hoặc là mắc về nỗi diễn đạt, dấu chấm, dấu phẩy, quy tắc viết hoa, cũng như là dùng từ không đúng. Theo bạn thì giữa một bài không có viết tắt và một bài viết tắt hay giữa một bài trình bày đẹp, ngắn gọn và một bài dài, khó hiểu thì bài nào xứng đáng được chọn hơn. Ừm có thể là giáo viên chỉ chọn những bài khó để tick vì nếu bài dễ thì ai cũng làm được mà.
Bạn ơi, trang HOC24 thành lập là để cùng nhau học tập, giúp đỡ nhau nhưng khúc mắc trong những bài học khó. Còn việc tíc để lấy điểm chỉ là động lực để các bạn học tốt hơn thôi. Quan trọng là các bạn học tập được những gì từ nhau, tiếp thu được những gì trên trang HOC24. Làm sao lại phải đố kị vì những thứ điểm đó chứ. Các thầy cô trên HOC24 cũng có nguyên tắc, xem xét những bài giải hay để tíc cho các bạn, giúp các bạn nhận biết những bài làm hay để học tập chứ cũng đâu phải để lấy điểm hỏi đáp đâu bạn.

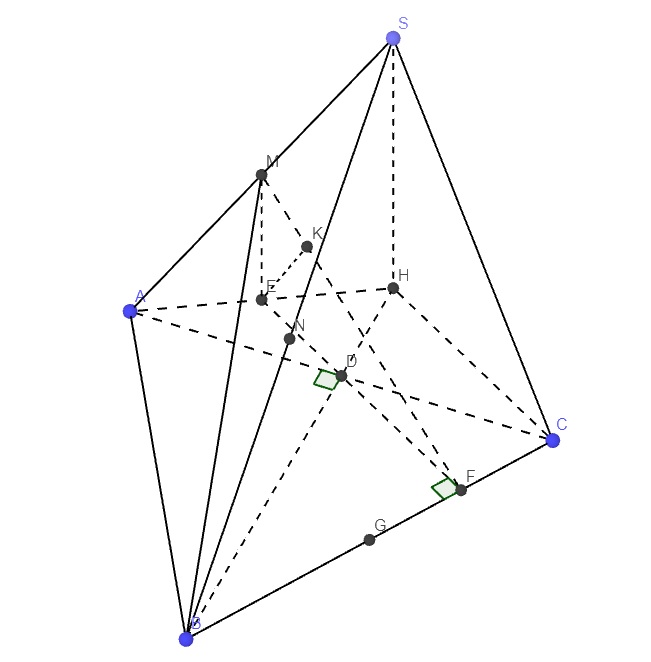
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)

Với n=0 \(\Rightarrow\) phương trình có 2 nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Với n \(\ne0\)
Để phương trình có nghiệm duy nhất \(\Leftrightarrow\dfrac{n}{2}\ne\dfrac{2}{n}\Rightarrow n^2\ne4\Rightarrow n\ne\pm2\)
Vậy hệ phương trình có nghiệm duy nhất \(\forall n\ne\pm2\)
cho mình hỏi có đúng với nghiệm nguyên không vì đề bài yêu cầu nghiệm nguyên ạ ?

76 successful
77 richness
78 musician
79 pollution
80 saving
81 unpleasant
82 misinformed
83 favorable
84 encouragement
85 qualified
86 traditionally
87 dressed
88 invention
89 musician
90 ability
91 nervousness
92 confidence
93 independently
94 endlessly
95 breakthrough
96 lessen
97 penniless
98 pursuit
99 Contended
100 situation
101 expectation
102 variety
103 logical

37 distinguish
38 illiteracy
39 energetic
40 disconnected
41 anxiety
42 mysteriously
43 significant
44 frightening
45 repeatedly
46 cancellation
47 disastifying
48 products
49 disagree
50 typicallu
51 socialize
52 vegetarian
53 entrance
54 modernized
55 income

Em ơi, em cần phương pháp giải dạng nào. và bài tập cụ thể là như nào vậy em, phải có đề bài cụ thể thì thầy cô mới hướng dẫn được em nhé