cho tam giac cân ABC(AB=AC).Từ B vẽ đường thẳng vuông góc với AB,từ C vẽ đường thẳng vuông goc với AC,chúng căt nhau ở E.Chứng minh rằng EA là tia phân giác của góc BEC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SV
27 tháng 1 2015
Gọi F là giao điểm của ED và BC.
Trong tam giác BCE thì CI và BA là hai đường cao cắt nhau tại D, nên D là trực tâm
Suy ra AF vuông góc với BC.
Tam giác BDF có góc B = 450, nên góc BDF = 450. Mà góc ADE = góc BDF vì đối đỉnh do đó góc ADE = 450.
Suy ra tam giác ADE vuông cân tại A. Vậy AD = AE
CM
22 tháng 4 2018
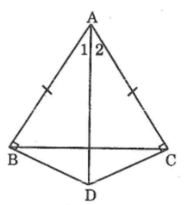
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A
NM
Nguyễn Minh Quang
Giáo viên
24 tháng 1 2021
câu a Do tam giác AFE có AH vừa là tia phân giác vừa là đường cao nên AFE cân tại A
b. Do KB song song với FE mà tam giác AFE cân tại A nên AKB cũng cân tại A
do đó KF=KA-AF=AB-AE=BE do đó ta có đpcm
c. DO FM//KB mà M lại là trung điểm của BC nên F là trung điểm CK do đó ta có
\(AC+AB=AC+AK=AF-FC+AF+KF=2AF=2AE\)
21 tháng 3 2021
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(Hai cạnh tương ứng)
MA
10 tháng 5 2015
Ta có hình vẽ
a)Xét tam giác BEMvà CFMta có
BM=CM(vì AM là trung tuyến ứng với BC)
Góc ABC=góc ACB(vì tam giác ABC cân ở A)
góc BEM=CFM(=90)
=>tam giácBEM=CFM(cạnh huyền-góc nhọn)
b) Từ câu a ta có Tam giác BEM=CFM
=>BE=FC(hai cạnh tương ứng)
ta có AE=AB-BE
AF=AC-CF
Mà AB=AC(tam giác ABC cân ở A)
BE=CF(như trên)
Vậy AE=AF
TRong 1 tam giác cân đường trung tuyến đồng thời là đường phân giác, đường trung trực,....
nên AM là phân giác góc A =>góc BAM=CAM
Xét tam giác AEI và AFI ta có
AI cạnh chung
AE=AF
góc BAM=CAM
=>tam giác AEM=AFM(c.g.c)
=>góc AIE=AIF(tương ứng)
Mà AIE+AIF=180do(kề bù)
=>AIE=AIF=180/2=90do
Vậy AM vuông góc với EF
c) theo câu a ta có tam giác BEM=CFM
=>ME=MF
vậy M thuộc phân giác góc A (1)
Xét tam giác vuông ABD và ACD có
AD cạnh chụng
góc BAM=CAM
=>tam giác ABD=ACD(cạnh huyền -góc nhọn)
=> DB=DC => D thuộc phân giác của góc A(2)
Từ (1) và (2) =>A;M;D thẳng hàng
ea la tia p/g cua BEC