Trong mp xOy, cho hai điểm B(-1;3) C(3;1), Tìm tọa độ điểm A sao cho tam giác ABC vuông cân tại A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi giao điểm là A, thay tọa độ tham số d1 vào d2:
\(t-2\left(2-t\right)+m=0\Leftrightarrow3t+m-4=0\Rightarrow t=\dfrac{-m+4}{3}\)
\(\Rightarrow A\left(\dfrac{-m+4}{3};\dfrac{m+2}{3}\right)\)
\(\Rightarrow OA=\sqrt{\left(\dfrac{-m+4}{3}\right)^2+\left(\dfrac{m+2}{3}\right)^2}=2\)
\(\Leftrightarrow m^2-2m-8=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)
b. Bạn không đưa 4 đáp án thì không ai trả lời được câu hỏi này. Có vô số đường thẳng cách đều 2 điểm, chia làm 2 loại: các đường thẳng song song với AB và các đường thẳng đi qua trung điểm của AB
c. Tương tự câu b, do 3 điểm ABC thẳng hàng nên có vô số đường thẳng thỏa mãn, là các đường thẳng song song với AB
b)
A. x-y+2=0
B. x+2y=0
C.2x-2y+10=0
D. x-y+100=0
c)
A. x-3y+4=0
B. -x+y+10=0
C. x+y=0
D. 5x-y+1=0

a) Ta có: O nằm trên đường trung trực của MN(gt)
nên OM=ON(1)
Ta có: O nằm trên đường trung trực của MP(gt)
nên OM=OP(2)
Từ (1) và (2) suy ra ON=OP
b) Xét ΔONM có OM=ON(cmt)
nên ΔOMN cân tại O(Định nghĩa tam giác cân)
mà Ox là đường trung trực ứng với cạnh đáy MN
nên Ox là tia phân giác của \(\widehat{MON}\)
Xét ΔOMP có OM=OP(cmt)
nên ΔOMP cân tại O(Định nghĩa tam giác cân)
mà Oy là đường trung trực ứng với cạnh đáy MP
nên Oy là tia phân giác của \(\widehat{POM}\)
Ta có: \(\widehat{NOM}+\widehat{POM}=\widehat{PON}\)
\(\Leftrightarrow\widehat{PON}=2\cdot\left(\widehat{xOM}+\widehat{yOM}\right)=2\cdot90^0=180^0\)
hay P,O,N thẳng hàng(đpcm)

Em viết đề bài sai lung tung cả: Bài 1. Thực chất yêu cầu là tỉ số lớn hơn hoặc bằng căn 2. Dấu bằng có thể xảy ra ví dụ xét hình vuông. Bài 2: Điểm M nằm trong góc, qua M kẻ đường thẳng ...
1. Để giải bài toán này ta cần một nhận xét đơn giản sau: Nếu tam giác \(ABC\) có góc \(\angle A\ge90^{\circ}\) và có cạnh \(AB\le AC\) thì \(\frac{BC}{AB}\ge\sqrt{2}.\)
Chứng minh nhận xét: Trên cạnh AC lấy X sao cho AB=AX, suy ra tam giác ABX vuông cân và do đó theo định lý Pitago \(BX^2=AB^2+AX^2=2AB^2\to BX=AB\sqrt{2}.\)
Mặt khác hoặc X trung C, khi đó BX=BC, hoặc tam giác \(\Delta BXC\) có góc ở X tù nên \(BC>BX\).
Vậy ta luôn có \(BC\ge AB\sqrt{2}\to\frac{BC}{AB}\ge\sqrt{2}.\)
Giải bài toán 1. Ta giả sử bốn điểm là A,B,C,D. Khi đó hoặc chúng là bốn đỉnh của một tứ giác lồi, hoặc một tứ giác lõm.
Trường hợp 1. Nếu ABCD là tứ giác lồi, vì tổng các góc trong một tứ giác là 360 nên không mất tính tổng quát ta có thể coi \(\angle B\ge90^{\circ}\). Áp dụng nhận xét cho tam giác ABC ta được \(\frac{BC}{AB}\ge\sqrt{2}\) hoặc \(\frac{BC}{AC}\ge\sqrt{2}\to\frac{M}{m}\ge\sqrt{2}.\) Ở đây kí hiệu M,m là độ dài đoạn lớn nhất và bé nhất.
Trường hợp 2. ABCD là tứ giác lõm, không mất tính tổng quát coi D nằm trong tam giác ABC. Khi đó trong ba góc \(\angle ADB,\angle BDC,\angle CDA\) có một góc tù. Giả sử góc \(\angle ADC>90^{\circ}\), suy ra \(\frac{AC}{AD}\ge\sqrt{2}\) hoặc \(\frac{AC}{CD}\ge\sqrt{2}\to\frac{M}{m}\ge\sqrt{2}.\)
Vậy ta có \(\frac{M}{m}\ge\sqrt{2}.\)
Bài toán 2. Cho góc vuông xOy, và điểm M nằm trong. Vẽ đường thẳng d cắt Ox,Oy ở A,B khác O. Tìm vị trí của đường thẳng d để
a)OAB có diện tích bé nhất
b)OA+OB nhỏ nhất.
Kí hiệu E,F là hình chiếu của M lên các cạnh Ox,Oy. Để cho tiện ta đặt \(a=FB,b=EA,x=ME,y=MF.\) Chú ý rằng \(x,y\) là các số dương không đổi. Từ \(\Delta MFB\sim\Delta AEM\to\) \(\frac{a}{y}=\frac{x}{b}\to ab=xy\). Theo bất đẳng thức Cô-Si thì \(a+b\ge2\sqrt{ab}=2\sqrt{xy}\to a+b+x+y\ge x+y+2\sqrt{xy}=\left(\sqrt{x}+\sqrt{y}\right)^2\)
\(\to OA+OB\ge\left(\sqrt{x}+\sqrt{y}\right)^2.\) Dấu bằng xảy ra khi và chỉ \(a=b=\sqrt{xy}.\) Khi đó trên Ox lấy A sao cho \(OA=x+\sqrt{xy}\), đường thẳng d qua AM sẽ thỏa mãn yêu cầu. Vậy giá trị bé nhất của \(OA+OB\) là \(\left(\sqrt{x}+\sqrt{y}\right)^2.\)
Chú ý rằng \(S_{OAB}=S_{OBM}+S_{OAM}=\frac{1}{2}x\left(a+y\right)+\frac{1}{2}y\left(x+b\right)=xy+\frac{1}{2}\left(xa+yb\right).\)
Theo bất đẳng thức Cô-Si \(xa+yb\ge2\sqrt{xayb}=2xy\to S_{OAB}\ge xy+xy=2xy.\) Dấu bằng xảy ra khi \(xa=yb,xy=ab\leftrightarrow b=x,a=y\leftrightarrow M\) là trung điểm \(AB.\)
Vậy giá trị bé nhất của diện tích tam giác \(OAB\) là \(2xy.\)

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)

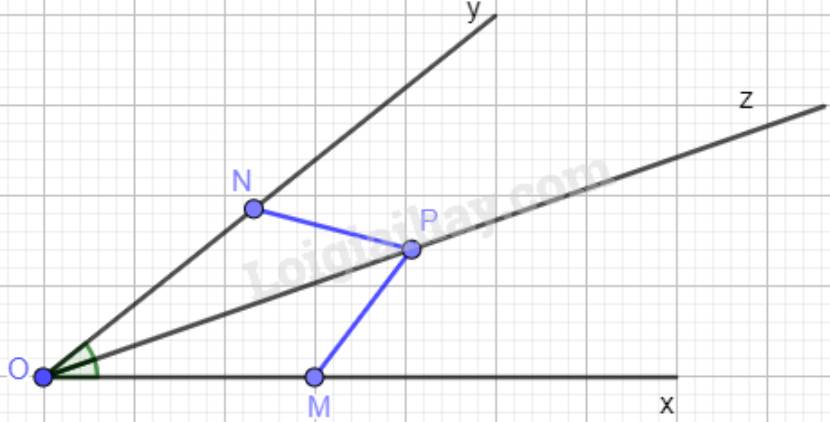
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)