Bài 4.(2.0điểm) Cho góc nhọn xOy. Trên tia đối của tia Ox lấy điểm A, trên tia đối của tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD và OB<OD, OA<OC.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm của AD và BC. Chứng minh: EAC = EBD.
c) Chứng minh: AB//CD.

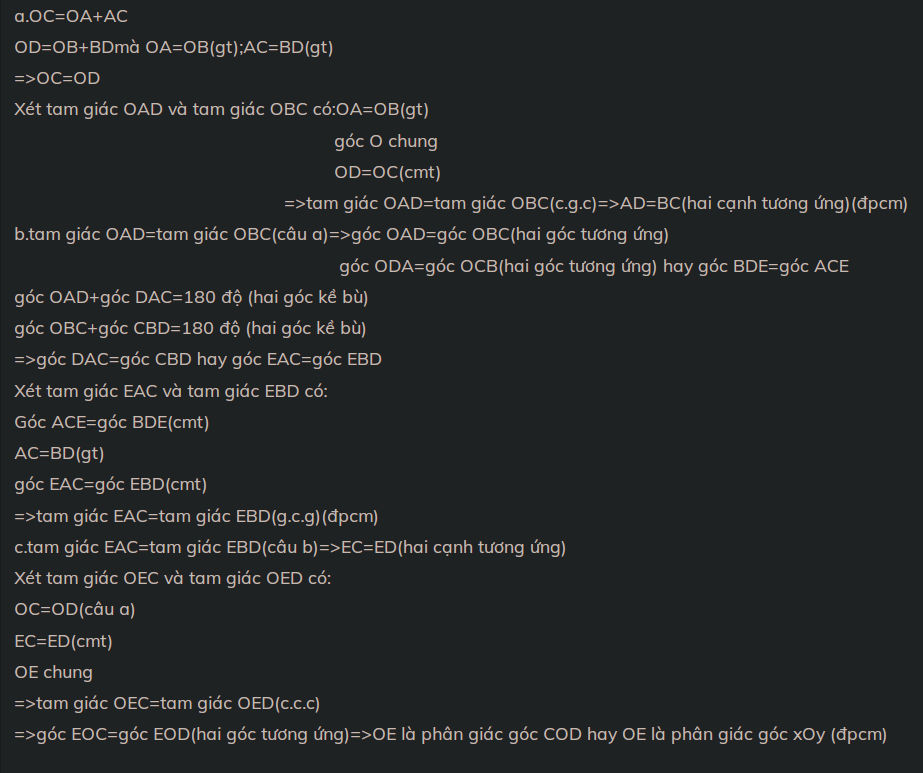
A B C D x y O E
Bài làm
a) Vì OA = OB
=> Tam giác OAB cân tại O
=> \(\widehat{DBA}=\widehat{CAB}\)
Xét tam giác ABC và tam giác BAD có:
AC = BD (giả thiết)
\(\widehat{DBA}=\widehat{CAB}\)
AB chung
=> Tam giác ABC = tam giác BAD (c.g.c)
=> BC = AD
b), c) Vì tam giác OAB cân tại O
=> \(\widehat{BAO}=\frac{180^0-\widehat{BOA}}{2}\) (1)
Ta có: BO + OD = BD
AO + OC = AC
Mà AO = OB, BD = AC
=> OD = OC
Vì tam giác OCD cân tại O (Do OD = OC)
=> \(\widehat{OCD}=\frac{180^0-\widehat{COD}}{2}\) (2)
Mà \(\widehat{BOA}=\widehat{COD}\)(đối nhau) (3)
Từ (1), (2) và (3) => \(\widehat{BAO}=\widehat{OCD}\)
Mà hai góc này ở vị trí đồng vị
=> AB // CD (đpcm)
=> ABCD là hình thang
Mà BC = AD (chứng minh trên)
=> ABCD là hình thang cân
=> \(\widehat{ABC}=\widehat{BAD}\)
Ta có: \(\widehat{ABE}+\widehat{ABC}=180^0\)
\(\widehat{BAE}+\widehat{BAD}=180^0\)
Mà \(\widehat{ABC}=\widehat{BAD}\)
=> \(\widehat{ABE}=\widehat{BAE}\)
=> Tam giác ABE cân tại E
=> AE = EB
Lại có: AE + AD = ED
EB + BC = EC
Mà AE = EB, AD = BC
=> ED = EC
Xét tam giác EAC và tam giác EBD có:
EC = ED (chứng minh trên)
\(\widehat{CED}\)chung
EB = EA (chứng minh tren)
=> Tam giác EAC = tam giác EBD (c.g.c) (đpcm)
P/S: Mình làm gộp câu b với câu c với nhau. Ở câu b), mình không biết là chứng minh góc hay tam giác, nên mình chứng minh tam giác, mà nếu chứng minh góc thì đơn giản hơn, mình trình bày nếu chứng minh góc đây nhé,
b), c) Vì tam giác OAB cân tại O
=> \(\widehat{BAO}=\frac{180^0-\widehat{BOA}}{2}\) (1)
Ta có: BO + OD = BD
AO + OC = AC
Mà AO = OB, BD = AC
=> OD = OC
Vì tam giác OCD cân tại O (Do OD = OC)
=> \(\widehat{OCD}=\frac{180^0-\widehat{COD}}{2}\) (2)
Mà \(\widehat{BOA}=\widehat{COD}\)(đối nhau) (3)
Từ (1), (2) và (3) => \(\widehat{BAO}=\widehat{OCD}\)
Mà hai góc này ở vị trí đồng vị
=> AB // CD (đpcm)
=> ABCD là hình thang
Mà BC = AD (chứng minh trên)
=> ABCD là hình thang cân
=> \(\widehat{ABC}=\widehat{BAD}\)
Ta có: \(\widehat{ABE}+\widehat{ABC}=180^0\)
\(\widehat{BAE}+\widehat{BAD}=180^0\)
Mà \(\widehat{ABC}=\widehat{BAD}\)
=> \(\widehat{ABE}=\widehat{BAE}\)
Lại có: \(\widehat{ABE}+\widehat{ABD}=\widehat{EBD}\)
\(\widehat{BAE}+\widehat{BAC}=\widehat{EAC}\)
Mà \(\widehat{ABE}=\widehat{BAE}\)(chứng minh trên)
\(\widehat{ABD}=\widehat{BAC}\)(do tam giác OAB cân tại O)
=> \(\widehat{EAC}=\widehat{EBD}\) (đpcm)
Và đây là cách giải nếu là chứng minh góc nha ^^