Cho a/b=c/d
CMR: 5.a+3.c/5.a-3.c= 5.b+3.d/5.b-3.d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
2: \(\dfrac{2a+b}{a-2b}=\dfrac{2\cdot bk+b}{bk-2b}=\dfrac{b\left(2k+1\right)}{b\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
\(\dfrac{2c+d}{c-2d}=\dfrac{2dk+d}{dk-2d}=\dfrac{d\left(2k+1\right)}{d\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
Do đó: \(\dfrac{2a+b}{a-2b}=\dfrac{2c+d}{c-2d}\)
3: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5\cdot bk+3b}{5dk+3d}=\dfrac{b\left(5k+3\right)}{d\left(5k+3\right)}=\dfrac{b}{d}\)
\(\dfrac{5a-3b}{5c-3d}=\dfrac{5\cdot bk-3b}{5\cdot dk-3d}=\dfrac{b\left(5k-3\right)}{d\left(5k-3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)


Ta có \(\frac{1}{a^3}+\frac{1}{a^3}+\frac{1}{b^3}\ge\frac{3}{a^2b}\)
\(\frac{1}{b^3}+\frac{1}{b^3}+\frac{1}{c^3}\ge\frac{3}{b^2c}\)
..............................
=> \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}+\frac{1}{d^3}\ge\frac{1}{a^2b}+\frac{1}{b^2c}+\frac{1}{c^2d}+\frac{1}{d^2a}\left(1\right)\)
Áp dụng bđt cosi ta có
\(\frac{a^2}{b^5}+\frac{1}{a^2b}\ge\frac{2}{b^3}\)
\(\frac{b^2}{c^5}+\frac{1}{b^2c}\ge\frac{2}{c^3}\)
\(\frac{c^2}{d^5}+\frac{1}{c^2d}\ge\frac{2}{d^3}\)
\(\frac{d^2}{a^5}+\frac{1}{d^2a}\ge\frac{2}{a^3}\)
Cộng vế của các bđt trên và kết hợp với (1)
=> ĐPCM
Dấu bằng xảy ra khi a=b=c

\(\frac{2a}{3b}=\frac{3b}{4c}=\frac{4c}{5d}=\frac{5d}{2a}=\frac{2a+3b+4c+5d}{3b+4c+5d+2a}=1\)
\(\Rightarrow\frac{2a}{3b}+\frac{3b}{4c}+\frac{4c}{5d}+\frac{5d}{2a}=4\)

Ta có:
Tập hợp A:
\(A=\left\{1;3;5;7;9\right\}\)
Tập hợp B:
\(B=\left\{0;1;2;4;5;6;8\right\}\)
Mà: \(C=A\cup B\)
\(\Rightarrow C=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
⇒ Chọn D
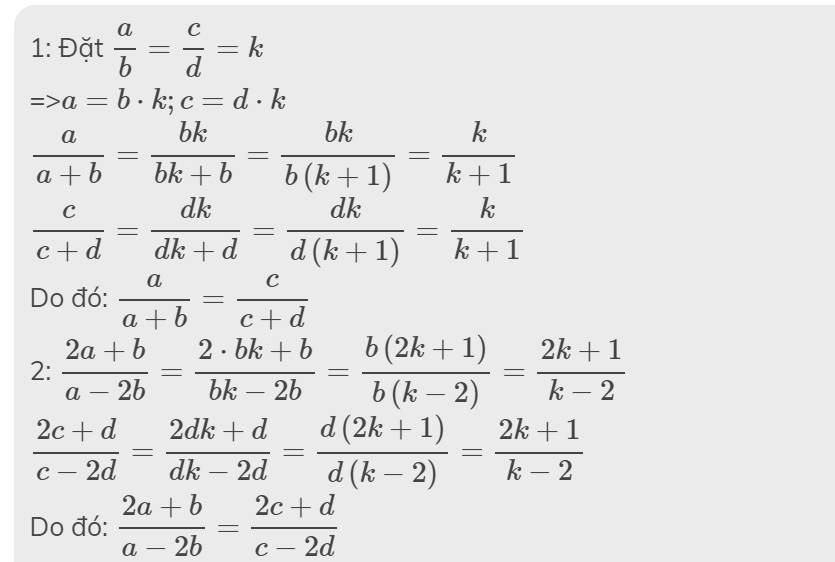
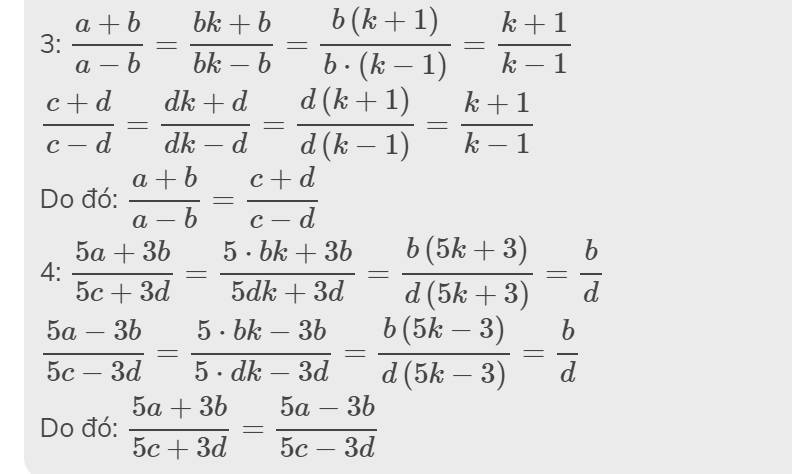
\(\frac{a}{b}=\frac{c}{d}=\frac{5a}{5b}=\frac{3c}{3d}=\frac{5a+3c}{5b+3d}=\frac{5a-3c}{5b-3d}\Rightarrow\frac{5a+3c}{5a-3c}=\frac{5b+3d}{5b-3d}\)