Cho s=1+2+22+23+...+299 so sánh S với 2100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
F
2
4 tháng 1 2021
Có : \(S=1+2+2^2+2^3+....+2^{99}\)
\(\Rightarrow2S=2+2^2+2^3+....+2^{100}\)
\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{100}\right)-\left(1+2+2^2+....+2^{99}\right)\)
\(\Rightarrow S=2^{100}-1< 2^{100}\)
Vậy \(S< 2^{100}\)
4 tháng 1 2021
S=1+2+22+23+....+299
⇒2S=2+22+23+....+2100
⇒2S−S=2100-1
S=2100-1
vì 2100 -1<2100
⇒S<2100
PL
4
T
14 tháng 7 2023
\(S=1+2+2^2+2^3+...+2^9\)
Đặt \(2S=2+2^2+2^3+2^4+...+2^{10}\)
\(2S-S=2^{10}-1\) hay \(S=2^{10}-1< 2^{10}\)
\(\Rightarrow\) \(2^{10}=2^2.2^8< 5.2^8\)
Vậy \(S< 5.2^8\)
\(#Tuyết\)
14 tháng 7 2023
2S=2+2^2+...+2^10
=>S=2^10-1=1023
5*2^8=256*5=1280
=>S<5*2^8
NN
2
BD
5 tháng 8 2023
\(A=2^{100}-2^{99}+2^{98}-2^{97}+....-2^3+2^2-2+1\\ A=\left(2^{100}+2^{98}+...+2\right)-\left(2^{99}+2^{97}+...+1\right)\)
Gọi \(\left(2^{100}+2^{98}+...+2\right)\)là B
\(B=\left(2^{100}+2^{98}+...+2\right)\\ 2B=2^{102}+2^{100}+.....+2^2\\ 2B-B=\left(2^{102}+2^{100}+.....+2^2\right)-\left(2^{100}+2^{98}+...+2\right)\\ B=2^{102}-2\)
Gọi \(\left(2^{99}+2^{97}+...+1\right)\) là C
\(C=\left(2^{99}+2^{97}+...+1\right)\\ 2C=2^{101}+2^{99}+....+2\\ 2C-C=\left(2^{101}+2^{99}+9^{97}+...+2\right)-\left(2^{99}+9^{97}+...+1\right)\\ C=2^{101}-1\)
\(A=B+C\\ =>A=2^{102}-2+2^{101}-1\\ A=2^{101}\left(2+1\right)-3\\ A=2^{101}\cdot3-3\\ A=3\cdot\left(2^{101}-1\right)\)
HQ
Hà Quang Minh
Giáo viên
5 tháng 8 2023
\(\dfrac{1}{2}A=2^{99}-2^{98}+...-1+\dfrac{1}{2}\\ \Rightarrow A-\dfrac{1}{2}A=2^{100}-\dfrac{1}{2}\\ \Rightarrow A=2^{101}-1\)
VT
5
LN
10 tháng 9 2023
S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)2�−�=(2+22+23+...+210)−(1+2+22+...+29)
\(S=2^{10}-1=2^2.2^8-1=4.2^8-1
HT
LN
11 tháng 9 2023
S=1+2+22+...+29�=1+2+22+...+29
2S=2(1+2+22+...+210)2�=2(1+2+22+...+210)
2S=2+22+23+...+292�=2+22+23+...+29
2S−S=(2+22+23+...+210)−(1+2+22+...+29)2�−�=(2+22+23+...+210)−(1+2+22+...+29)
\(S=2^{10}-1=2^2.2^8-1=4.2^8-1
PT
2
22 tháng 1 2024
Sửa đề: \(S=2^{100}-2^{99}+2^{98}-...+2^2-2\)
=>\(2\cdot S=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(2S+S=2^{100}-2^{99}+2^{98}-...+2^2-2+2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
=>\(3S=2^{101}-2\)
=>\(S=\dfrac{2^{101}-2}{3}\)
AB
1
11 tháng 9 2021
\(A=2+2^2+2^3+2^4+...+2^{99}+2^{100}\)
\(\Rightarrow2A=2^2+2^3+2^4+...+2^{100}+2^{101}\)
\(\Rightarrow A=2A-A=2^2+2^3+2^4+...+2^{100}+2^{101}-2-2^2-2^3-2^4-...-2^{99}-2^{100}=2^{101}-2\)
CM
19 tháng 4 2018
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
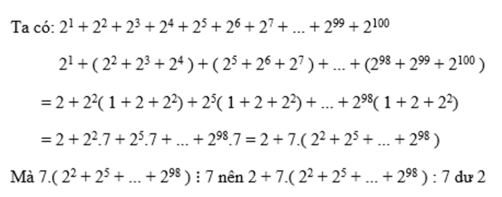
Lời giải:
$S=1+2+2^2+2^3+2^4....+2^{99}$
$2S=2+2^2+2^3+....+2^{100}$
Trừ theo vế ta có:
$2S-S=(2+2^2+2^3+...+2^{100})-(1+2+2^3+..+2^{99})=2^{100}-1$
$S=2^{100}-1< 2^{100}$