Cho ΔABC (góc A = 900), lấy E є BC. Lấy D, F lần lượt là các điểm đối xứng với E qua các trục AB, AC.
a. CMR: D, F đối xứng nhau qua A.
b. ΔDEF là tam giác gì? Vì sao?
c. CMR: BC = BD + CF.
d. ◊BDFC là hình gì? Vì sao?
e. E ở vị trí nào trên BC để ◊BDFC là hình bình hành?
f. ΔABC cần điều kiện gì để khi đó E ở vị trí nào trên BC để ◊BDFC là hình chữ nhật.

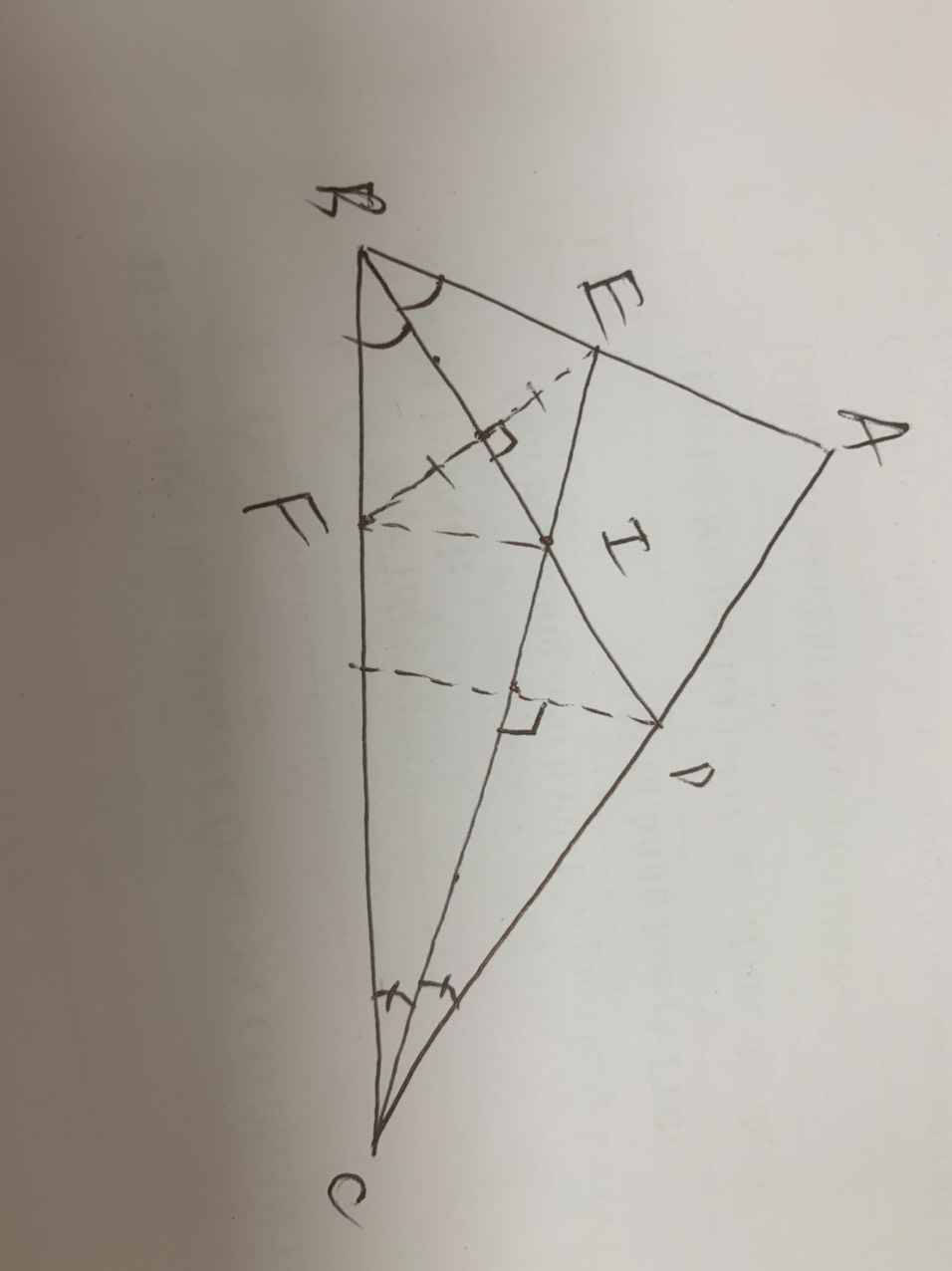 Với đề bài cho như bạn viết thì câu a thì chứng minh đúng được. Còn câu b thì IF không thể là phân giác của góc BCI được. Câu c là F không thể đối xứng được D qua CI (hình vẽ minh hoạ, luôn tồn tại điểm K trên BC khác điển F)
Với đề bài cho như bạn viết thì câu a thì chứng minh đúng được. Còn câu b thì IF không thể là phân giác của góc BCI được. Câu c là F không thể đối xứng được D qua CI (hình vẽ minh hoạ, luôn tồn tại điểm K trên BC khác điển F)
Gọi M , B là trung điểm của DE , EF
a) Xét hai tam giác vuông \(\Delta AEM\)và \(\Delta ADM\)có :
AM chung ; EM = DM
=> \(\Delta AEM=\Delta ADM\)( hai cạnh góc vuông )
=> AE = AD và \(\widehat{A2}\)\(=\widehat{A1}\)(1)
Chứng minh tương tự , ta có : AE = AF và \(\widehat{A4}\)\(=\widehat{A3}\)(2)
Từ (1) , (2) suy ra :
AE = AD = AF và \(\widehat{A1}+\widehat{A2}+\widehat{A3}+\widehat{A4}=2.\left(\widehat{A2}+\widehat{A3}\right)=2.90^O=180^O\)
=> AD = AF và D,A,F thẳng hàng
=> D và F đối xứng nhau qua A ( đpcm )
b) F đối xứng với E qua N => EN\(\perp\)AC , tương tự EM\(\perp\)EN
=> AMEN là hình chữ nhật => EM\(\perp\)EN
=>\(\Delta DEF\)là tam giác vuông tại E
c) Xét \(\Delta ABD\)và \(\Delta ABE\)ta có :
AB chung ; AD = AE ; \(\widehat{A1}=\widehat{A2}\)
=> \(\Delta ABD=\Delta ABE\)( c.g.c ) => BD = BE
Tương tự ta chứng minh được CE = CF
Suy ra : BD + CF = BE + CE = BC ( đpcm )
d) EN \(||\)AB => \(\widehat{E1}=\widehat{B1}\)mà \(\widehat{B1}=\widehat{B2}\) ( do \(\Delta ABD=\Delta ABE\)) và \(\widehat{E1}=\widehat{F1}\)
=> \(\widehat{B2}=\widehat{F1}\)
Lại có AB \(||\)EF => BD \(||\)CF
=> BDFC là hình thang ( CF , BD là hai cạnh đáy )
e) Để BDCF là hình bình hành thì CF = BD mà CF = CE ; BD = BE
=> CE = BE <=> E là trung điểm của BC
f) Để BDFC là hình chữ nhật thì BD\(\perp\)BC mà \(\widehat{B2}=\widehat{B1}\)
=> \(\widehat{B2}=\widehat{B1}=45^O\Rightarrow\Delta ABC\)vuông cân ở A
Đồng thời kết hợp với điều kiện để BDFC là hình bình hành tức E là trung điểm của BC
Khi đó BDFC sẽ là hình chữ nhật