cho A(-1 -3) B(1 1) và C(3 -1).tìm tọa độ điểm D để ABCD là hình thang cân biết AB//CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PA
1
5 tháng 6 2016
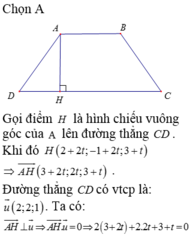
-viết pt DC
- gọi điểm D theo DC
- theo t/c hình thang ta có : AC=BD => điểm D
CM
28 tháng 10 2017
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
LA
0
2 tháng 9 2021
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
TA
15 tháng 4 2016
Gọi \(\overrightarrow{n}=\left(a,b\right)\) là vectơ pháp tuyến của CD (\(a^2+b^2\ne0\)
Ta có phương trình CD : \(ax+by+a+b=0\)
\(S_{BCD}=S_{ACD}=8\Rightarrow d\left(A;CD\right)=\frac{2.S}{CD}=2\Rightarrow d\left(M.CD\right)=1\)
\(\Rightarrow\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=1\Leftrightarrow3a^2-4ab=0\)\(\rightarrow\begin{cases}a=0;b=1\\a=4;b=3\end{cases}\)\(\rightarrow\begin{cases}CD:y+1=0\\CD:4x+3y+7=0\end{cases}\)
Với \(CD:y+1=0\rightarrow D\left(d;-1\right);CD^2=4.AB^2=64\Leftrightarrow\begin{cases}d=7\\d=-9:L\end{cases}\)
\(D\left(7;-1\right);\overrightarrow{AB}=\frac{1}{2}\overrightarrow{DC}=\left(-4;0\right)\rightarrow B\left(-9;-3\right)\)
Với \(CD:4x+3y+7=0\rightarrow D\left(d;\frac{-4d-7}{3}\right)\rightarrow CD^2=\frac{25\left(d+1\right)^2}{9}=64\) (loại)