Question

[Trần Thị Ngọc Phú]

Cho lăng trụ ABC.A'B'C' với AB=a,BC=2a,ABC=60°, hình chiếu A' lên mặt phẳng ABC trùng với trọng tâm G của tam giác ABC; góc giữa AA' và mp (ABC) bằng 60°.Tính thể tích khối chóp A'ABC và khoảng cách từ G đến mp (A'BC)

Answer 1

[Nguyễn Việt Lâm]

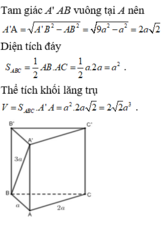
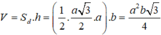
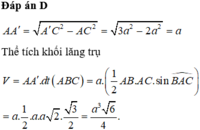
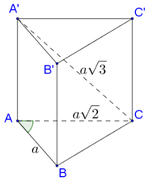
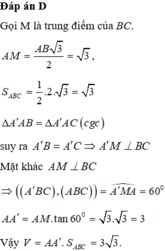
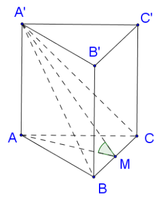
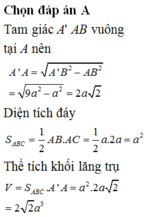
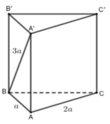
Gọi M là trung điểm BC \(\Rightarrow BM=\dfrac{BC}{2}=a\)

\(\Rightarrow\Delta ABM\) đều \(\Rightarrow AM=a\Rightarrow AG=\dfrac{2}{3}AM=\dfrac{2a}{3}\)

\(A'G\perp\left(ABC\right)\Rightarrow\widehat{A'AG}=60^0\)

\(\Rightarrow A'G=AG.tan60^0=\dfrac{2a\sqrt{3}}{3}\)

\(S_{ABC}=\dfrac{1}{2}AB.BC.sinB=...\)

\(\Rightarrow V_{A'ABC}=\dfrac{1}{3}A'G.S_{ABC}=...\)

\(A'B=\sqrt{A'G^2+BG^2}=\sqrt{A'G^2+AB^2+AG^2-2AB.AG.cos60^0}=...\)

\(A'C=\sqrt{A'G^2+CG^2}=\sqrt{A'G^2+\dfrac{2}{3}\left(BC^2+\left(\dfrac{AB}{2}\right)^2-2.BC.\dfrac{AB}{2}.cos60^0\right)}=...\)

\(\Rightarrow S_{\Delta A'BC}\) theo công thức Herong

\(\Rightarrow d\left(G;\left(A'BC\right)\right)=\dfrac{1}{3}d\left(A;\left(A'BC\right)\right)=\dfrac{1}{3}.\dfrac{3V_{A'ABC}}{S_{\Delta A'BC}}=...\)