Tính diện tích toàn phần của hình chóp cụt đều theo các kích thước cho trên hình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
PT
1
CM
18 tháng 8 2017
Hình vẽ đã cho là hình chóp có 3 mặt xung quanh và mặt đáy là tam giác đều bằng nhau có cạnh là a.Áp dụng định lí pi-ta-go vào tam giác vuông CIA,ta có: A C 2 = A I 2 + C I 2
Suy ra: C I 2 = A C 2 - A I 2 = a 2 - a / 2 2 = 3 a 2 / 4
Vậy CI = a 3 2
Ta có: S A B C =1/2. a .a 3 2 = a 2 3 4 (đvdt)
Vậy S T P =4. a 2 3 4 = a 2 3 (đvdt)
CM
6 tháng 10 2019
Đường cao hình chóp bằng: 13 2 - 5 2 = 144 = 12 cm
Diện tích đáy bằng:S = 10.10 = 100 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .100.12=400 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd = 10.2.13 = 260 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 260 + 100 = 360 ( c m 2 )
CM
20 tháng 6 2017
Đường cao hình chóp bằng: 5 2 - 3 2 = 25 - 9 = 16 = 4 cm
Diện tích đáy bằng:S = 6.6 = 36 ( c m 2 )
Thể tích hình chóp bằng : V=1/3 S.h=1/3 .36.4=48 ( c m 3 )
Diện tích xung quanh bằng: S x q = Pd=2.6.5=60 ( c m 2 )
Diện tích toàn phần là : S T P = S x q + S đ á y = 60 + 36 = 96 ( c m 2 )
CM
13 tháng 7 2017
Thể tích phần hình hộp chữ nhật:
V = 5.5.5 = 75 (đvtt)
Ta có: IJ = AA' ⇒ IJ = 3
OI = IJ = 3
SJ = 9 ⇒ SO = 3
Suy ra: S A 1 = A 1 A ' ; S D 1 = D 1 D '
Khi đó hình vuông A 1 B 1 C 1 D 1 có cạnh A 1 B 1 = 1/2 A'B' = 2,5
Thể tích hình chóp đều S. A'B'C'D' là:
V= 1/3 (5.5).6 = 50 (đvtt)
Thể tích hình chóp đều A 1 B 1 C 1 D 1 là:
V= 1/3(2,5.2,5).3 = 6,25 (đvtt)
Thể tích hình chóp cụt A'B'C'D'. A 1 B 1 C 1 D 1 là:
V = 50 – 6,25 = 43,75 (đvtt)
Thể tích của một trụ bê tông là:
V = 43,75 + 75 = 118,75 (đvtt).
SG
1
24 tháng 9 2017
V = \(\dfrac{1}{3}\)S . h = \(\dfrac{1}{3}\)a.h.h = \(\dfrac{1}{3}\)ah2
10 tháng 5 2017
Thể tích hình hộp chữ nhật là V1 = 5.5.3 = 75
Vì OI = IJ , IJ = AA' = 3 và SJ = 9 nên OI = 3 và SO = 3
\(\Rightarrow A_1B_1C_1D_1\) là hình vuông cạnh 2,5
Vậy thể tích hình chóp S.A1B1C1D1 là :
\(V_2=\dfrac{1}{3}.3.2,5.2,5=6,25\)
Thể tích hình chóp S.A'B'C'D' là :
\(V_3=\dfrac{1}{3}.6.5.5=50\)
Vậy thể tích cần tính là : \(V=V_1+V_3-V_2=118,75\)
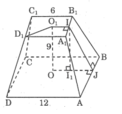
Ta có:A1D1 =6 ⇒ O 1 I =3
AD=12 ⇒ OJ=6
Kẻ II1 ⊥ OJ ta có: I 1 J =3
Áp dụng định lí pi-ta-go vào
tam giác vuông I I 1 J ,ta có:
I J 2 = I I 1 2 + I 1 J 2 = 9 2 + 3 2 =90
Suy ra: IJ = 90
Diện tích mặt một bên là một hình thang bằng: S =1/2 (6+12). 90 =9 90 (đvdt)
Diện tích xung quanh bằng : S x q = 4.9 90 =36 90 (đvdt)
Diện tích đáy trên bằng :S = 6.6=36(đvdt)
Diện tích đáy dưới bằng :S=12.12=144 (đvdt)
Diện tích toàn phần của hình chóp cụt bằng: S T P = 36 90 +36+144=(36 90 +180) (đvdt)