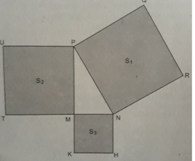
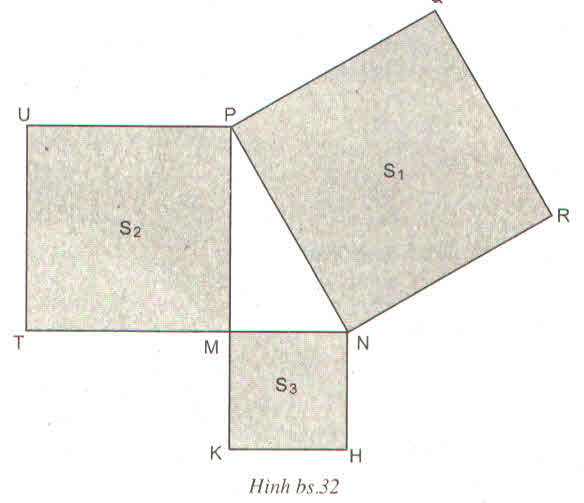
Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông, còn S 1 , S 2 , S 3 tương ứng là diện tích của một hình). Quan hệ nào sau đây là đúng?
(A) S 3 + S 2 = S 1
(B) S 3 2 + S 2 2 = S 1 2
(C) S 3 + S 2 > S 1
(D) S 3 2 + S 2 2 < S 1 2

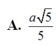
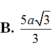
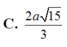
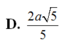
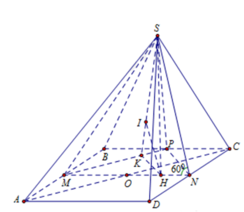
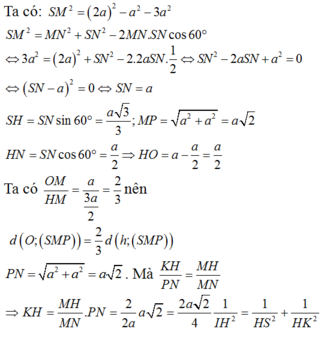
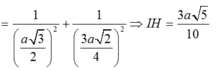



Chọn A