Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}s_1=\dfrac{b}{a}x+\dfrac{c}{a}z\\s_2=\dfrac{a}{b}x+\dfrac{c}{b}y\\s_3=\dfrac{a}{c}z+\dfrac{b}{c}y\\x+y+z=5\end{matrix}\right.\) \(\left\{{}\begin{matrix}s_1+s_2+s_3=\left(\dfrac{b}{a}+\dfrac{a}{b}\right)x+\left(\dfrac{c}{b}+\dfrac{b}{c}\right)y+\left(\dfrac{a}{c}+\dfrac{c}{a}\right)z\\a,b,c\in N\left(sao\right)\\\dfrac{b}{a}+\dfrac{a}{b}\ge2;\left(\dfrac{c}{b}+\dfrac{b}{c}\right)\ge2;\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\ge2\\x+y+z=5\end{matrix}\right.\)
\(s_1+s_2+s_3\ge2x+2y+2z\ge2\left(x+y+z\right)=2.5=10\)

Chờ chờ chờ.... Vẫn chưa có ai trả lời cho heo Dương, haizz...
Bye!
Trịnh Ngọc Hân
Bà cj on sớm z! Lúc đó e dậy rồi nhưng.......đg chơi game 
 !kkk
!kkk

* Phương án đúng:
(D). S
* Giải thích:
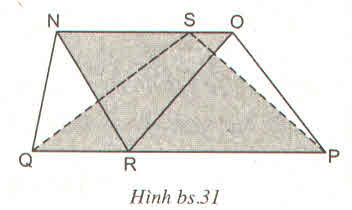
Đường cao của hình thang cũng chính bằng độ dài đường cao của hai tam giác QSP và NRO.
Gọi độ dài đường cao là h (h>0)
SQSP= \(\dfrac{1}{2}.h.QP\)
SNRO= \(\dfrac{1}{2}.h.NO\)
SNRO+SQSP=\(\dfrac{1}{2}.h.NO\)+\(\dfrac{1}{2}.h.QP\)= \(\dfrac{1}{2}.h.\left(NO+QP\right)\) (1)
Ta có:
SNOPQ=S=\(\left(NO+QP\right).h.\dfrac{1}{2}\) (2)
Từ (1) và (2) => SNRO+SQSP=S=\(\dfrac{1}{2}.h.\left(NO+QP\right)\)

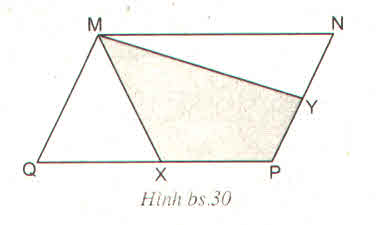
Kẻ đường chéo MP
Ta được SMQX= SMPX
SMNY=SMPY
=> SMXPY= SMPX + SMPY
Khi đó \(S_{MXPY}=\dfrac{1}{2}S\)
Nhớ tick nhé !
Sau khi kẻ đường thẳng MP ta có:
\(\Delta MPQ=\Delta MPN\) (cạnh-cạnh-cạnh)
=> \(\dfrac{1}{2}\)SMPQ = \(\dfrac{1}{2}S_{MPN}\)
hay \(\Delta MPX=\Delta MPY\).
Vì \(S_{MPX}+S_{MPY}=S_{MXPY}=S_{MXQ}+S_{MYN}\) nên SMXPY = \(\dfrac{1}{2}S\).
Vậy SMXPY = \(\dfrac{1}{2}S\).

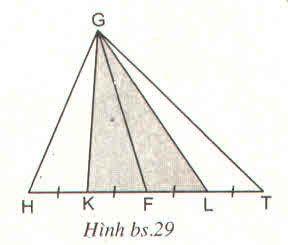
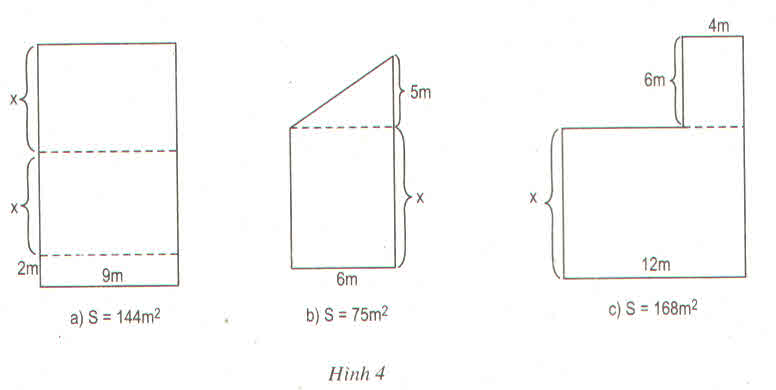
a) 9(2x+2)=144
18x +18=144
18x = 126
x = 7
Vậy x = 7m
b) 6x+15 = 75
6x = 60
x = 10
Vậy x = 10m
c) 12x+24 = 168
12x = 144
x =12
Vậy x = 12m.

* Phương án đúng:
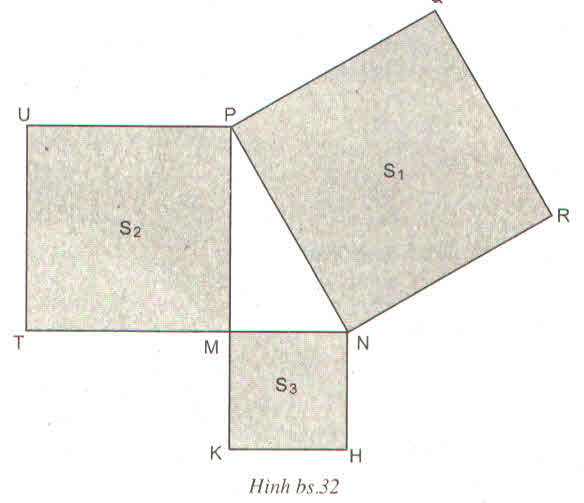
Quan hệ đúng của diện tích 3 hình vuông là:
(A). \(S_3+S_2=S_1\)
(A) S3+S2=S1