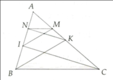
Cho tam giác ABC . AB = AC. AB song song MN.(M thuộc BC; N thuộc AC). Tam giác AMN là tam giác gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BK
1 tháng 7 2023
Ta có thể giải bài toán này bằng cách sử dụng công thức diện tích của hình bình hành, và áp dụng định lí hai đường cao trong tam giác để tính diện tích tam giác ABC.
Đầu tiên, ta cần tính diện tích tam giác ABC. Ta sẽ sử dụng định lí hai đường cao trong tam giác ABC để tính toán. Gọi H là hạt giác của góc A trong tam giác ABC, và gọi AH là đường cao kẻ từ A xuống BC. Ta sẽ sử dụng định lí hai đường cao trong tam giác ABC để tính diện tích của tam giác này:
$S_{ABC} = \frac{1}{2}AH \cdot BC$
Tiếp theo, ta cần tính diện tích của hình bình hành AEMK. Để làm điều này, ta sử dụng công thức diện tích của hình bình hành:
$S_{AEMK} = AE \cdot MK$
Ta có thể tính được AE và MK bằng cách sử dụng các hệ số tỉ lệ. Gọi x là độ dài BM, ta có:
$AE = \frac{AB}{BC} \cdot BM = \frac{S}{S_{ABC}} \cdot x$
$MK = \frac{MC}{BC} \cdot BM = \frac{S - SMCKS}{S_{ABC}} \cdot x$
Lưu ý rằng ta sử dụng diện tích của hình bình hành để tính các hệ số tỉ lệ này.
Cuối cùng, ta có thể tính diện tích của hình bình hành AEMK bằng cách thay các giá trị được tính toán vào công thức diện tích của hình bình hành:
$S_{AEMK} = AE \cdot MK = \frac{S}{S_{ABC}} \cdot x \cdot \frac{S - SMCKS}{S_{ABC}} \cdot x = \frac{S(S-SMCKS)}{S_{ABC}^2} \cdot x^2$
Vậy diện tích của hình bình hành AEMK là $\frac{S(S-SMCKS)}{S_{ABC}^2} \cdot x^2$.
VT
1
3 tháng 12 2015
tự vẽ hình nha
ta có ab=ac mà bm=cm
suy ra AM=AN
xét tam giác ABC có
AM=AN
BN=CN
suy ra MN là đường trung bình của tam giác ABC
suy ra MN song song với BC và MN =\(\frac{1}{2}\)BC
Vậy MN song song với BC
1 tháng 11 2023
a: Xét tứ giác BMNP có
BM//NP
NM//BP
Do đó: BMNP là hình bình hành
Xét ΔABC có
N là trung điểm của CA
NP//AB
Do đó: P là trung điểm của BC
b: Sửa đề; HB//AP
Xét ΔABC có
N là trung điểm của AC
NM//BC
Do đó: M là trung điểm của AB
Xét tứ giác AHBP có
M là trung điểm chung của AB và HP
=>AHBP là hình bình hành